7.2 離散選択モデル
7.2.1 線形確率モデル
選択肢の持つ属性によって消費者の選択行動がどのように変化するかを、統計的に分析・説明するためには、被説明変数に選択結果をとり、説明変数に選択肢属性を取る以下のような回帰モデルを考える。なお、簡単化のために単回帰モデルで本アプローチを紹介しているが、以下の議論は任意の \(k\) 個の説明変数を含む重回帰モデルに応用することができる。
\[ y_i=\beta_0+\beta_1x_i+e_i, \] ただし、\(y\) は特定の製品を購入したか(\(y_i=1\))、購入していないか(\(y_i=0\))を表しており、\(x_i\) は価格を表しているとする。分析においては \(y_i\) と \(x_i\)についての情報を含むデータセットを用いて、パラメータ \(\beta_0\) と \(\beta_1\) を推定する。通常、(他の要素が一定である場合)価格が上がると製品を購入(選択)する確率は下がると考えられるので、\(\beta_1<0\) が予測される。このように消費者の選択を捉えた分析においては、被説明変数がダミー変数である回帰モデルを考える必要がある。しかしながら、ダミー変数のような離散変数を被説明変数に用いる場合には注意も必要である。
被説明変数がダミー変数であるOLS回帰モデルは線形確率モデル(Linear Probability Model: LPM)と呼ばれる。ただし、\(y\) が2値しか取らないため、\(\beta_1\) は、「\(x_i\) が1単位変化した際の \(y\) の変化」として解釈することはできない。
ここで、誤差項の条件付き期待値について 0 であるという仮定(\(E(e_i|x_i)=0\))に基づくと、\(y_i\) の条件付き期待値について以下を得る。
\[ E(y_i|x_i)=\beta_0+\beta_1x_i \]
ここで、\(y\) は 0 か 1 を取るダミー変数なので、\(P(y_i = 1|x_i)= E(y_i|x_i)\) と示すことができる(Wooldridge, 2012)。したがってLPMでは、以下のように線形モデル化したものだと理解できる。 \[ P(y_i = 1|x_i)=\beta_0+\beta_1x_i \]
このとき、\(P(y_i = 1|x_i)\) は反応確率(response probability)や成功確率(probability of success)と呼ばれる。また、確率の合計は 1 になるため、\(P(y_i = 0|x_i)=1-P(y_i = 1|x_i)\) もまた \(x_i\) に関する線形の関数になる。LPMにおいて定数項(\(\beta_0\))は \(x\) が0のときの反応確率を表しており、傾きの係数 \(\beta_1\) は \(x_i\) の変化に伴う反応確率の変化を表していると解釈できる。より具体的には、\(\beta_1\) は以下のように表現できる。
\[ \Delta P(y_i = 1|x_i)=\Delta\beta_1x_i \]
このことから、\(y\) の予測値(\(\hat{y_i} = \hat{\beta}_0+\hat{\beta}_1x_i\))も線形回帰モデルと同様に示すことができる。したがって、係数の解釈について注意が必要ではあるものの、LPMによる推定結果も線形回帰モデル同様の含意を提供する。特に、複数の説明変数を採用することで、他の変数を固定したうえで説明変数の変化に伴う反応確率の変化を捉えることができる。そのため、LPMによって着目する変数が反応確率へ与える影響を検証することができる。
しかしながら、LPMの推定結果には注意も必要である。具体的には、以下の2点について問題が生じる。
- 誤差項の分散が不均一になる。
- 予測値が論理的整合性を満たさなくなる。
第一の問題点については、LPMで推定してしまうことで、OLS推定量が好ましい性質を持つための仮定(均一分散)を満たさないことにつながる。分散が均一であるとは、誤差項の分散がどの観測個体 \(i\) に対しても同じ大きさであることを指す。そのため、特定の主体だけ誤差項の分散が大きい場合や、\(x\) の値の変化に伴って誤差項の分散が大きくなるような状態ではこの仮定は満たされず、分散不均一であると言われる。
ここで、上記のモデルの誤差項は \(e_i= y_i - (\beta_0+\beta_1x_i)\) である。ここで、\(y_i\) の条件付き期待値を \(P_i=E(y_i|x_i)=P(y_i = 1|x_i)=\beta_0+\beta_1x_i\) と定義すると、誤差項の分散は \(Var(e_i|x_i)=P_i(1-P_i)\) となることが知られている(西山ほか,2019)。\(P_i\) の大きさはその定義より各主体によって \(x_i\) に依存する形で変化することが伺える。そのため、LPMによる推定では、分散不均一の問題が生じるといえる。しかしながらこの問題は通常、分散不均一に対して頑健な標準誤差(例えば、ホワイトの標準誤差)を用いた分析を用いることで対応される。
第二に予測値の論理的整合性について説明する。LPM推定によって得た \(y\) の予測値は、反応確率の予測値を表すため、 \(y\) の予測値は 0 から 1 の間に収まらないといけない。しかし、LPMでは予測値が負の値を取ったり、1 を上回ることもある。言い換えると確率の定義に反するような、論理的に整合的ではない予測値を返してしまう。ここで、以下のような簡単な人工データを用いて、LPMによる分析を実行してみる。下記df1の成果変数(Y)はダミー変数であり、説明変数(X)は連続変数だとする。これを線形モデルで回帰し、予測値を出力してみる。すると、1つ目と4つ目の観測は負の値、7つ目と8つ目の観測は1を越える予測値を得たことが伺える。
df1 <- data.frame(Y = c(0, 0, 0, 0, 0, 1, 1, 1, 1),
X = c(3.4, 5.22, 7.06, 2.81, 4.11, 10.34, 13.67, 15.99, 9.09))
lpm1 <- lm(Y ~ X, data = df1)
pred_lpm1 <- predict(lpm1)
pred_lpm1 ## 1 2 3 4 5 6
## -0.006342894 0.173357681 0.355032986 -0.064597476 0.063760077 0.678888967
## 7 8 9
## 1.007681776 1.236750640 0.555468243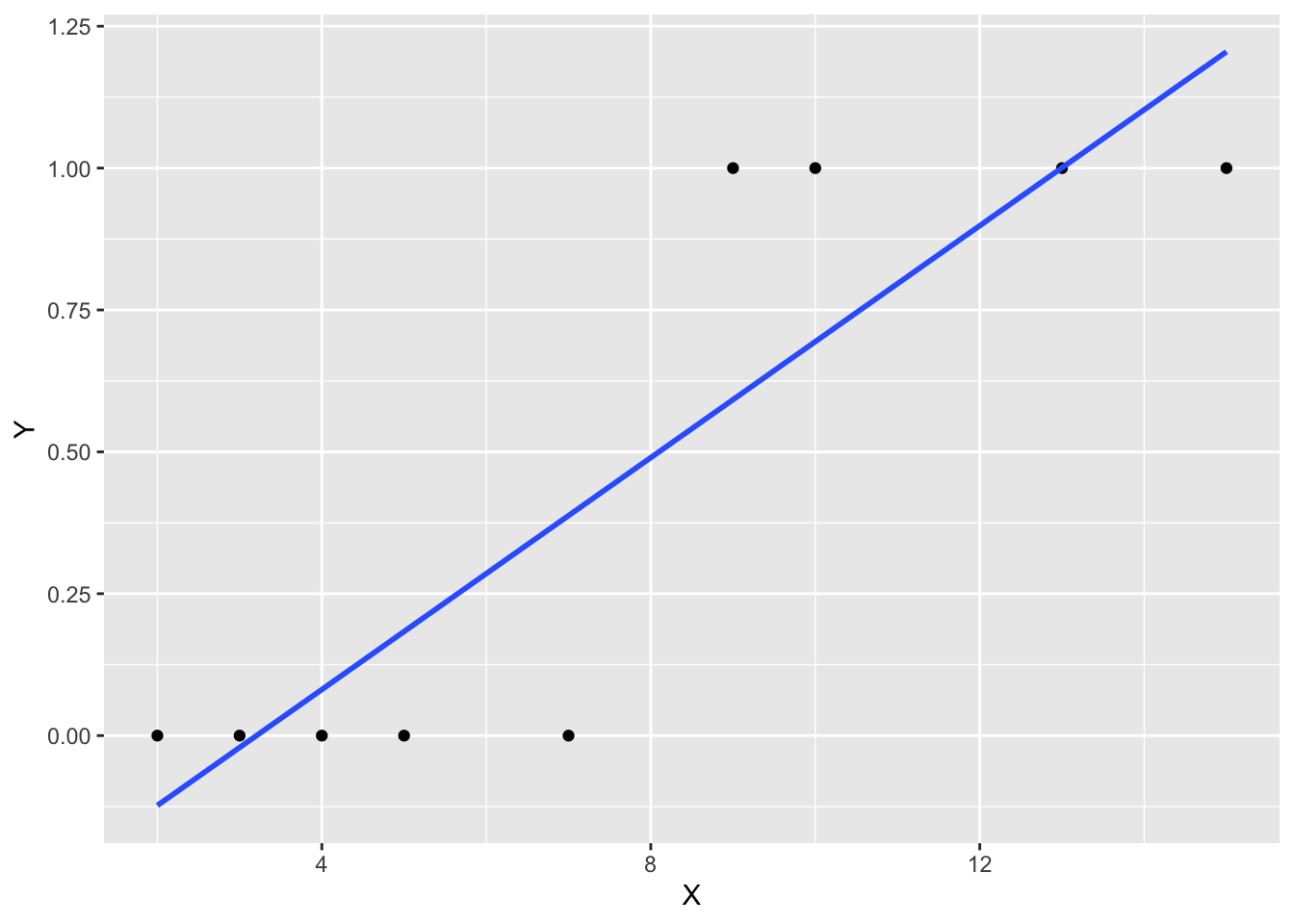
Figure 7.1: LPM と回帰直線
そのため、予測を重視する研究を行う場合には、LPMは適さないことが多い。その一方で変数間の関係を検証することを目的とする場合には、大きな問題にはならないとする主張もある(西山ほか, 2019)。言い換えると、ある説明変数が選択確率に与える影響を統計的に検証するという目的のもとでは、LPMでも対応可能である。操作変数法や固定効果推定といった発展的な手法が線形モデルでは開発されており、LPMではこれらの手法を応用することができることもこの考え方に影響を与えている。
7.2.2 プロビットモデルとロジットモデル*{#logitprobit}
任意の \(k\) 個の説明変数を用いたLPMの反応確率は、 \[ P_i=E(y_i|x_{1i},...,x_{ki})=P(y_i = 1|x_{1i},...,x_{ki})=\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki} \] となる。このモデルを分析するうえで線形確率モデル(LPM)が有する問題のひとつは、この確率が 0 から 1 の範囲を越えてしまうことにあった。この問題は、\(y\)(選択)と \(x\)(説明変数)との関係を線形で捉えることが原因となっている。そのため、0 から 1 の範囲を超えないように、何らかの累積分布関数を用いて非線形で分析を行う(回帰直線ではなく、回帰曲線を引く)ことで、この問題を克服する事ができる。
非線形なモデルとして分析する場合、回帰モデルによる反応確率は以下のように示すことができる。
\[ P(y_i = 1|x_{1i},...,x_{ki})=F\left(\beta_0+\beta_1x_i+...+\beta_kx_{ki}\right) \] ただし、\(F(\cdot)\)は選択(反応確率)と説明変数を非線形な形で結びつけるためのなんらかの関数である。ここで採用する\(F(\cdot)\)によって回帰曲線の形状が決まる。
例えば、図 7.2は図7.1との対比として(説明変数が一つのモデルを)非線形でのモデル化を示したものである。図 7.2のように、非線形の近似曲線で回帰分析を行うことで、確率を意味する予測値が0から1の範囲に収まる。
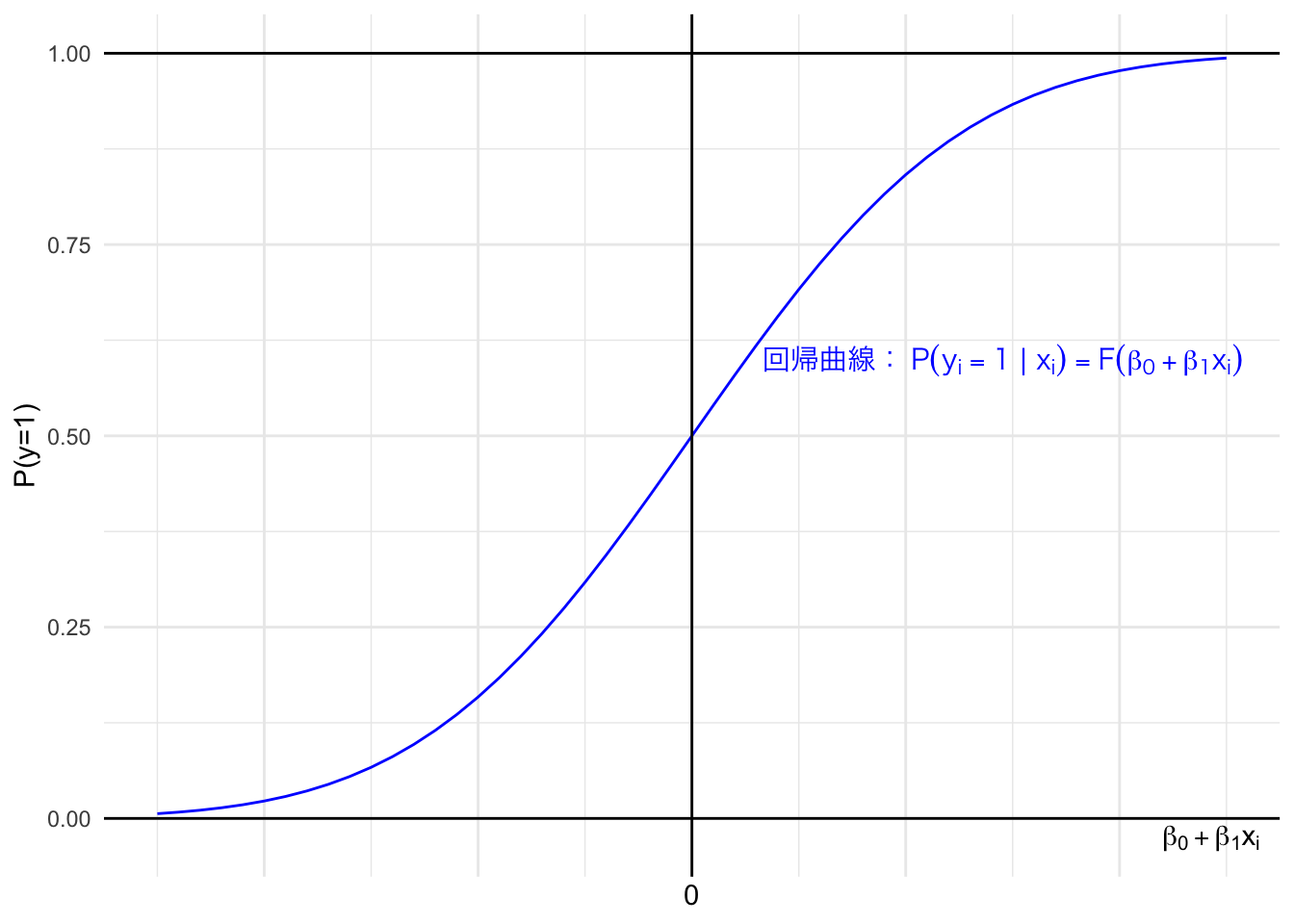
Figure 7.2: 非線形での近似イメージ
このときに用いる関数形として一般的なものが、標準正規分布の累積分布関数である。累積分布関数は、確率密度関数を積分していくことで得ることができ、0 を下限、1 を上限とする分布である。
標準正規分布の累積分布関数を\(\Phi\)(ファイ)で示すと、反応確率は以下のように表すことができる12。
\[ P(y_i=1|x_{1i},...,x_{ki})=\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})=\int^{\beta_0+\sum^k_{j =1}\beta_jx_{ji}}_{-\infty}\phi(z)~dz \]
一方で、\(P(y_i=0|x_{1i},...,x_{ki})\)については、以下が成り立つ。 \[ P(y_i=0|x_{1i},...,x_{ki})=1-P(y_i=1|x_{1i},...,x_{ki})=1-\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}) \] これにより、選択肢を選ぶことへの条件付き確率と選ばないことへの条件付き確率を、回帰モデルと標準正規分布の累積分布関数との関係から定義する事ができた。これを \(y_i=1\) か \(y_i=0\) という値を取る事象に対応させるため、ベルヌーイ確率関数13に代入すると、以下のような確率密度関数を考えることができる。
\[\begin{equation} P(y_i|x_{1i},...,x_{ki})=\\ \Big(\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}) \Big)^{y_i}\times \Big(1-\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}) \Big)^{1-y_i} \tag{7.1} \end{equation}\]
このように、選択行動に対して標準正規分布の累積分布関数を仮定して定式化するモデルを「プロビットモデル」と呼ぶ。また、選択モデルでは標準正規分布ではなく、ロジスティック分布の累積分布関数を用いた定式化を行う「ロジットモデル」を用いることも多い。ロジットモデルでは、ロジスティック分布の累積分布関数(\(\Lambda(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})\))を用いて、以下のような密度関数を用いる。
\[ P(y_i|x_{1i},...,x_{ki}) =\Lambda(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})=\frac{\exp(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})}{1+\exp(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})} \]
ロジットモデルでは、回帰モデル(\(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}\))の値が大きくなると反応確率が 1 に近づき、小さくなると 0 に近づくという性質を持っており、取りうる区間も 0 から 1 の間に限定されている。この点において、ロジットモデルはプロビットモデルと同様の特徴を持っている。そのうえでロジットモデルは分析における数値計算がプロビットモデルよりも容易であり、これまで広く使われてきたという経緯がある。コンピュータの性能が高まった近年ではプロビットモデルの使用が増えてきたものの、過去の研究との比較やこれまでの研究蓄積、慣習と言った側面を重視し、引き続きロジットモデルが使われることも多い。
7.2.3 潜在変数アプローチによる説明*{#latentApproach}
これまでは、「選択」という点に着目し、ベルヌーイ確率関数を用いてプロビットモデルを導出する方法を紹介した。一方で、選択という離散的な変数の背後に、観察できない連続的な変数(潜在変数: latent variable)が存在するという視点からモデル化を説明することも可能である。このような考え方を潜在変数アプローチと呼ぶ。マーケティング領域の論文やテキストでは、この潜在変数アプローチに基づく選択モデルの記述や紹介も行われるため、本書では、先述のプロビットモデルと潜在変数アプローチにより導出されたモデルが一致することを示す。
ここで、\(y_i^*\) という(観察可能な説明変数とは異なる)連続的な潜在変数を考え、以下のような回帰モデルを考える。
\[ y_i^*=\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}+e_i \]
ただし、この誤差項 \(e_i\) は標準正規分布に従い、\(e_i|x_{1i},...,x_{ki}~\sim N(0,1)\)を満たすと考える。
この時、\(y_i^*\) がある閾値を越えたならば(観察可能な)被説明変数は 1 をとり、越えない場合は被説明変数が 0 をとる、というような潜在変数と被説明変数との関係を考える。プロビットモデルでは具体的に、以下のような関係を仮定する。
\[ \begin{aligned} y_i= \left\{ \begin{array}{ll} 0 & ~\text{if}~~y_i^*\leq0 \\ 1 & ~\text{if}~~y_i^*>0 \end{array} \right. \end{aligned} \]
そのため、\(P(y_i=1|x_{1i},...,x_{ki})=P(y_i^*>0|x_{1i},...,x_{ki})\)や、\(P(y_i=0|x_{1i},...,x_{ki})=P(y_i^*\leq0|x_{1i},...,x_{ki})\) と示せることがわかる。この性質を利用して、選択しないことへの条件付き確率 \(P(y_i=0|x_{1i},...,x_{ki})\) は以下のように標準正規分布の累積分布関数を用いて表現できる(西山ほか, 2019, p.339)。
\[ \begin{align} P(y_i=0|x_{1i},...,x_{ki})&=P(y_i^*\leq0|x_{1i},...,x_{ki})\\ &= P(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}+e_i\leq0|x_{1i},...,x_{ki})\\ &=P(e_i\leq -\beta_0-\beta_1x_{1i}-...-\beta_kx_{ki}|x_{1i},...,x_{ki})\\ &=\Phi(-\beta_0-\beta_1x_{1i}-...-\beta_kx_{ki}) \end{align} \] 標準正規分布はその性質より、0を中心として左右対称な確率密度関数を持つ。そのため、\(e_i\) が \((-\beta_0-\beta_1x_{1i}-...-\beta_kx_{ki})\) 以下の値を取る確率と、\((\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki})\) 以上の値を取る確率は等しくなるため、以下を得る。
\[ P(y_i=0|x_{1i},...,x_{ki})=1-\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}) \] また、\(P(y_i=1|x_{1i},...,x_{ki})=1-P(y_i=0|x_{1i},...,x_{ki})\) であるため、反応確率は以下のように示すことができる。
\[ P(y_i=1|x_{1i},...,x_{ki})=\Phi(\beta_0+\beta_1x_{1i}+...+\beta_kx_{ki}) \] したがって、潜在変数アプローチでも通常のプロビットモデルと一致するモデルを得ることができた。