4.11 検定力分析とサンプルサイズ

統計的検定を行う場合、サンプルサイズの多さが実務的含意の弊害になりうるという議論も存在する。例えば、平均の差の検定においてサンプルサイズが著しく多いと、実務的にはあまり意味を持たない極めて小さな差であっても、「統計的に有意な差」として判断される事がある。このような弊害を避けるために、検定力分析と呼ばれる分析枠組みからサンプルサイズを計算する方法が用いられる（Cohen, 1988）。

ここでは、以下のような帰無仮説と対立仮説を用いる平均の差の検定を例に取りこのアプローチによるサンプルサイズの検討を紹介する。

\[ H_0:~~\mu_1=\mu_2\\ H_1:~~\mu_1\neq\mu_2 \] 検定力分析では、検定力と効果量という指標を用いる。検定力は第二種の誤りを犯す確率 \(\beta\) を用いて \(1-\beta\) と定義される。概念的に説明すると検定力とは、「母集団において 差があるとき，サンプルにおいて有意な結果が得られる確率」といえる（南風原, 2002, p.143）。一方で効果量は、サンプルサイズで変化することのない、標準化された効果の大きさについての指標である（水元・竹内, 2008）。先述の通り、サンプルサイズが大きいと、この効果量が小さくても統計的に有意な差があると判断されることもある。そのため、効果量を捉えることで実務的にどのような差があるのかを議論することが可能になる。なお、平均の差の検定においては、0.2、0.5、0.8をそれぞれ小さい、中くらい、大きい、に対応する効果量の目安として捉えられている（水本・竹内, 2008）。

検定力分析の枠組みでは、有意水準（\(\alpha\)）、検定力（\(1-\beta\)）、効果量（\(d\)）、サンプルサイズ（\(n\)）の4つの指標については、他の3つが定まると残りの1つの指標も自動的に求まるという関係を有する（水本・竹内, 2008）。検定力分析においては元々、分析における有意水準、効果量、サンプルサイズから分析の検定力を計算する方法として用いられてきた。しかしながら、上述の各指標同士の関係から、自身が想定する分析・検定の条件（\(\alpha\)、\(1-\beta\)、\(d\)）を指定することで、その条件を満たす \(n\) を求めることも可能である。この枠組みを採用することで、自身の求める大きさの効果量（例えば、\(d=0.8\)）を想定する条件（\(\alpha\)、\(1-\beta\)）で検定するために必要な \(n\)を逆算することが可能になる。

ここでは、検定力分析の詳細な計算方法について省略し、Rを用いた分析方法を紹介する。具体的な計算は、pwr::pwr.t.test() というパッケージおよび関数を用いる。なお、pwr には他にも様々な分析モデルに対応するサンプルサイズの計算が可能である。まずは、以下の通りパッケージをインストールし読み込む。

install.packages("pwr")
library(pwr)

ここでは、先行研究で推奨されている\(\alpha=0.05\)（引数では sig.level）、\(1-\beta=0.8\)（引数では power）という水準を用いて、平均の差の検定を行う場合のサンプルサイズを以下のように求める（Cohen, 1988）。

est_n <- pwr.t.test(d=0.8, power=0.8, sig.level=0.05)
est_n

## 
##      Two-sample t test power calculation 
## 
##               n = 25.52458
##               d = 0.8
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

出力結果の通り、上記の条件に基づくサンプルサイズは各グループ26人ずつであるとわかる。そのため、2グループ間の比較を行う場合のサンプルサイズの合計は52となる。また、検定力とサンプルサイズの関係について、plot() 関数を用いて以下のように出力することも可能である。

plot(est_n)

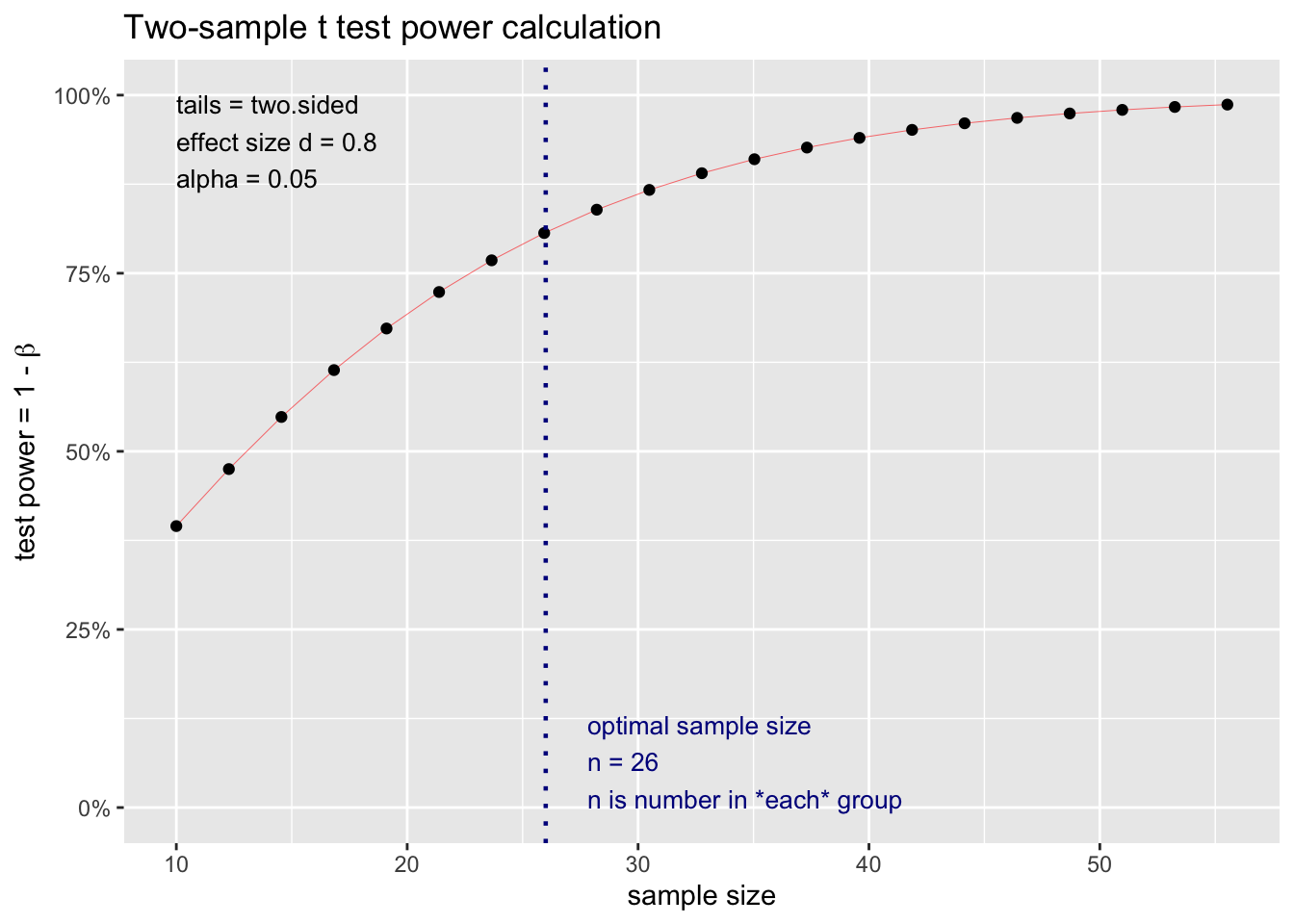
なお、pwr.t.test() 関数内の引数設定次第で、検定力を計算することも可能である。 例えば、\(d=0.8\), \(n=30\), \(\alpha=0.05\) の場合の検定力は以下のように計算できる。

pwr.t.test(d=0.8, n=26, sig.level=0.05)

## 
##      Two-sample t test power calculation 
## 
##               n = 26
##               d = 0.8
##       sig.level = 0.05
##           power = 0.8074866
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

そのため、研究者が採用した検定の条件や、分析結果としての効果量が算出できれば、その検定における検定力も同じ関数から計算可能であることが伺えた。