5.3 単回帰モデルと予測値
回帰分析絵では、二つの異なる変数 \(y,~x\) の関係を \(\small y=f(x)\) のように\(y\)を\(x\)の関数(\(f(x)\))で示すというアイディアで分析を行う。このとき \(y\) を「被説明変数(Explained variable)もしくは従属変数(dependent variable)」、\(x\) を「説明変数(Explaining variable)もしくは独立変数(independent variable)」という。そして、被説明変数と説明変数の関係を特定化した式のことを一般的に回帰モデルという。最も基本的な関数型の特定方法は以下のような一次関数による特定化である。
\[ y=\beta_0+\beta_1x \] このとき、\(\small \beta_0\) は切片、\(\small \beta_1\) は傾きを表す係数であり、回帰係数と呼ばれる。
回帰モデルは線形の関係を捉えているものの、実際にデータを入手し散布図を作成すると、以下のように、直線とは異なる結果を得る。そのため、上記のモデルは正確な表現でないことがわかる。
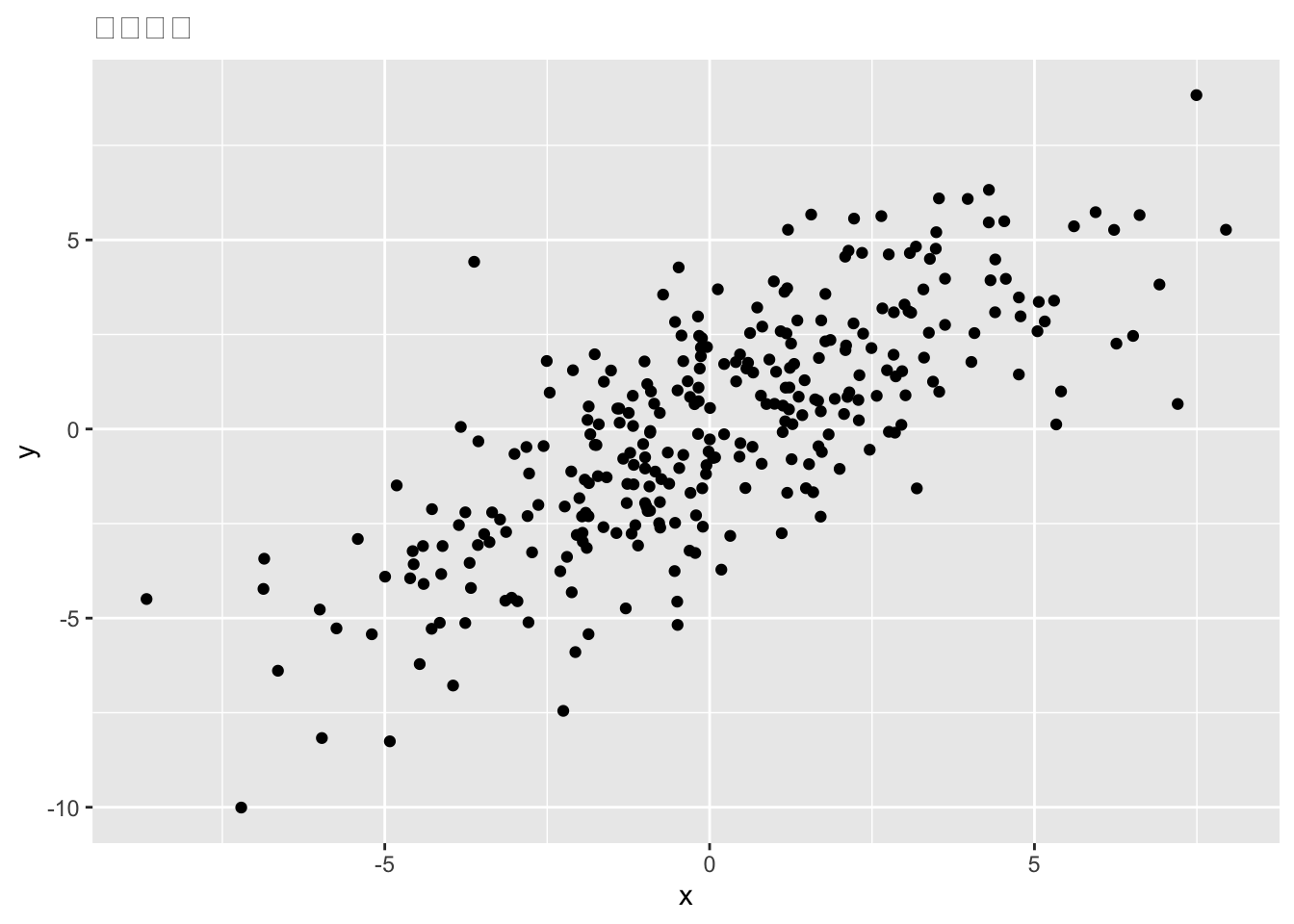
分析者がデータとして得る情報は、\(y\) や \(x\) の実現値であり、回帰モデルの切片や傾きの値は直接はわからない。そこで、モデルで捉えた直線と実現値のズレを考え、得たデータから回帰モデルのパラメータ(係数)を推定するという方針をとる。モデルで捉えた直線による(係数の推定値に基づく)\(y\) と\(x\) の関係は、\(\small x=x_i\) のとき、\(y_i\) の予測値である\(\small \hat{y}_i\)(ワイハット)と、係数の推定値 \(\small \hat{\beta}_0\)、 \(\small \hat{\beta}_1\) を用いて以下のように定義できる。
\[ \hat{y}_i=\hat{\beta}_0+ \hat{\beta}_1 x_i \]
係数の推定値 \(\small \hat{\beta}_0\) と \(\small \hat{\beta}_1\) を求めるための計算方法は、(最尤法や積率法など)いくつかあるものの、本書では最小二乗法(Ordinary least square: OLS)という方法に着目し紹介する。OLS推定量(OLS Estimator: OLSE)の求め方の直感は、以下の図の通り、観測値と回帰直線間の距離の合計(残差平方和)を最小にするように計算される。
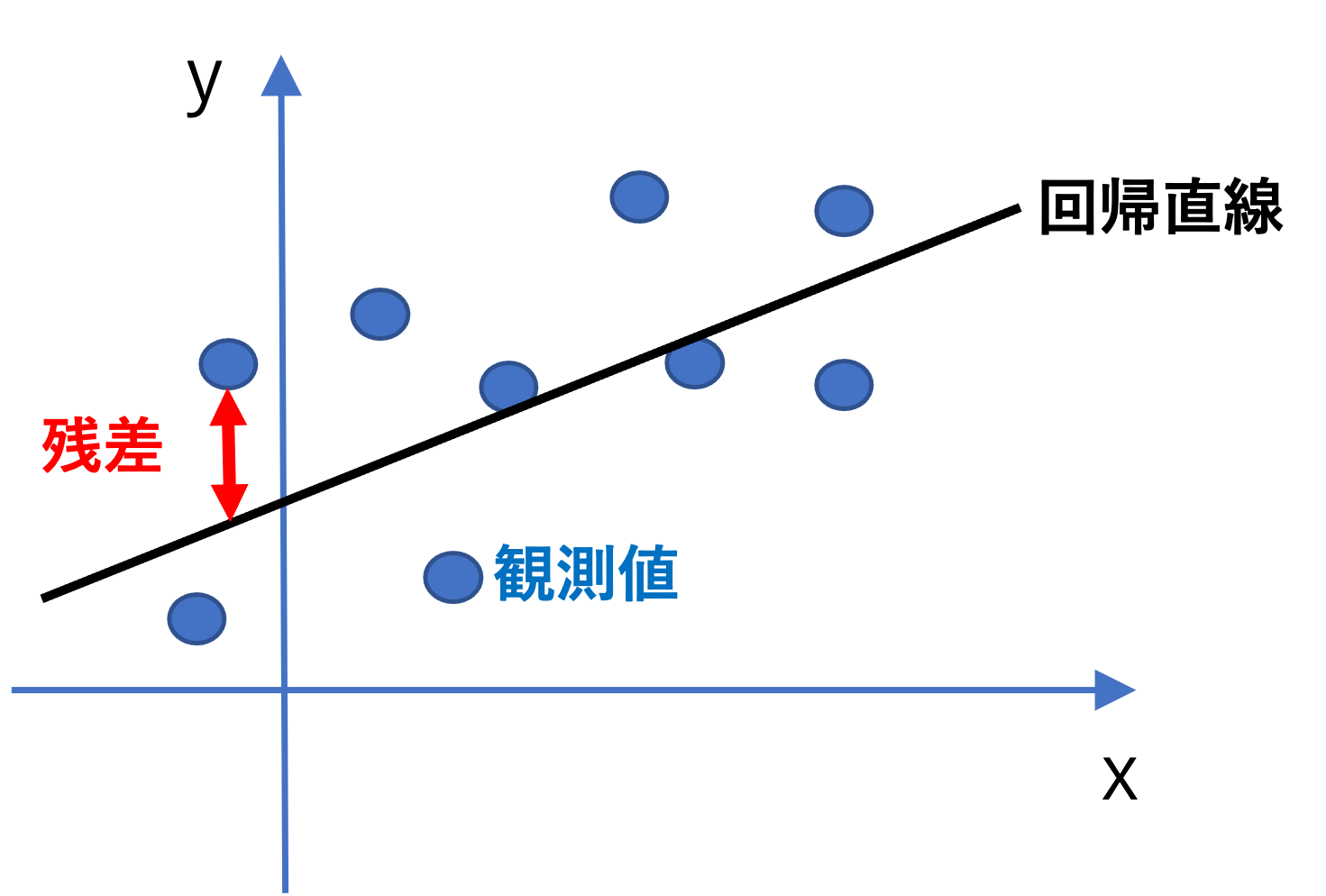
予測値のモデルで示されているのは、データを分析した結果求めたOLSEに基づく説明変数 \(x_i\) と、\(\small \hat{y}_i\) との関係である。\(\small \hat{y}_i\) は被説明変数 \(y_i\) の「予測値(predicted value)」や「理論値(fitted value)」と呼ばれるものであり、\(y_i\) の観測値とは異なる値であることに注意が必要である。
Rによる回帰分析は、lm()という関数(linear model)を用いて簡単に実行できる。この関数内では、lm(y ~ x, data = df) という要領で、説明変数と被説明変数を \(\sim\)(チルダ)で繋いでモデルを指定する。例えば、先程の企業データにおける2019年の観測を用いて、従業員数と売上高の関係について分析するためには、以下のように分析を実行する。
## (Intercept) emp
## 22113.98050 58.14081分析の結果、定数項(Intercept)は 22809.7 で、傾きは 58.1 であることがわかった。つまり、従業員数を一単位増やすと、売上高が58.1(百万円)増えることを示唆している。仮に従業員数が10人であれば、売上高の「予測値」は以下のように計算できる。
\[ 22695.0=22114.0+58.1\times 10 \]
回帰分析による予測の精度を調べるために、分析したモデルがどの程度被説明変数全体の分散を説明しているか、という指標によってモデルの適合度を測る。一般的には、決定係数(\(\small R^2\))という指標によってモデル適合度が示される。\(\small R^2\) は以下のように定義される。
\[ R^2=1-\frac{\sum(y_i-\hat{y}_i)^2}{\sum(y_i-\bar{y})^2}=\frac{\sum(\hat{y}_i-\bar{y})^2}{\sum(y_i-\bar{y})^2} \]
この指標は、被説明変数の分散を説明変数がどの程度説明するかの割合を表しており、0以上1以下の値を取る。例えば \(\small R^2\) が0.80であるならば、被説明変数の変動の80%をモデルが説明しているということになる。そのため、\(\small R^2\) は、回帰モデルの説明力として解釈される。しかしながら、予測という目的に対して近年は、機械学習などの発展的な手法が応用される事が多く、\(\small R^2\) を軸に予測を行うことは少なくなってきている。
また、予測ではなく説明変数の効果(係数)についての検証や解釈に関心がある場合、回帰分析における \(\small R^2\) の重要性は低くなる。特に、ビジネス分野における研究では、係数の推定や検定に焦点をあわせることが多い。本書においても、予測よりも係数に関する検証を重視する立場を取る。社会科学領域での分析では、\(\small R^2\) が低くなることは珍しくない。そんな中で、「\(\small R^2\) が低いからその回帰分析結果は意味がない」ということにはならない。研究者の目的が、関心のある変数同士(例、市場志向と企業成果)の関係性(有意性や影響の強さ)を検証したいというものである場合、仮に \(\small R^2\) が低くても、きちんと両変数の関係を分析できる調査設計や分析を実行しているならば、その検証は有意義なものになる。つまりここで強調したいのは、係数の検証や解釈を重視して研究を行う場合、「\(\small R^2\) がいくつ以上(以下)だから良い(ダメ)」という議論は目的と整合的ではなく、重要ではなくなるということである。
本節では、OLSを中心にデータから回帰係数を推定するプロセスに目を向け、予測値と決定係数について紹介した。しかしながら、先述の通り我々は多くの場合特定の変数が成果変数に与える影響の検証に関心がある。次節では確率的な視点から理論的に回帰分析を理解する事により、回帰分析の結果の解釈についてより詳しく学ぶ。
5.3.1 企業データを用いた回帰分析の実行
Rで回帰係数の検定結果を得るのは非常に簡単である。 lm() 関数の実行結果をストアしたオブジェクトに対して、summary() 関数を実行することで統計的検定結果を得ることができる。先程分析した reg1 を再度利用すると、以下のような結果を得る。
##
## Call:
## lm(formula = sales ~ emp, data = firmdata19)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1834902 -280228 -34549 136598 3292521
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 22113.980 89224.761 0.248 0.805
## emp 58.141 2.569 22.628 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 875800 on 144 degrees of freedom
## Multiple R-squared: 0.7805, Adjusted R-squared: 0.779
## F-statistic: 512 on 1 and 144 DF, p-value: < 2.2e-16回帰係数の推定と検定に関する結果は Coefficients: の下に記載されている。推定・検定結果は表のような形式で表示されており、Estimate の列は回帰係数の推定結果、Std. Error は標準誤差(詳細は省略するが、誤差項の分散推定量の平方根)、 t valueはt値、 Pr(>|t|)はp値をそれぞれ示している。そして、出力結果下欄には決定係数(R-squared)や自由度調整済み決定係数(Adjusted R-squared)、F検定結果、といったモデル適合度に関する結果が提示されている。
上記の結果を解釈するために、回帰分析における検定について説明する。ソフトウェアで自動的に出力される統計的仮説検定は、基本的には以下の帰無仮説と対立仮説を採用したものである(添字は省略)。 \[ H_0:\beta=0,~~H_1:\beta\neq0 \] なお、R以外のソフトウェアを用いて回帰分析を実行しても係数に関する検定結果を返すが、通常はこの帰無仮説を採用した検定結果を出力する。
検定では、以下のような検定統計量を用いる。
\[ t=\frac{\hat{\beta}-\beta}{se(\hat{\beta})} \]
\(H_0\) が正しい(\(\small \beta=0\))と仮定すると、検定統計量 t は計算可能であり、自由度(\(\small n-2\))のt分布に従う。検定の手順は 4.8.1節で紹介したのと同様、有意確率に基づく臨界値を定めた後、t 値を計算し、棄却域と採択域のどちらに入るのかを確認する。
\[ \begin{cases} |t|>t_{\alpha/2}(n-2) & \Rightarrow \text{H0を棄却する。}\\ |t|\leq t_{\alpha/2}(n-2)& \Rightarrow \text{H0を採択する。} \end{cases} \]
これを踏まえて分析結果を確認すると、emp が sales に与える影響(係数: 58.132)は有意に0とは異なると理解できる。また、切片の係数推定値(Intercept)は大きな値を取っているが、統計的には0ではないとは言えないことが示されている。この項は、従業員数が0のときの企業の売上を示しており、この結果が統計的に有意ではないということは、我々の直感とも整合的である。
上記の検定によって、どうやら emp の係数は0ではなさそうだということが示唆された。では、具体的にどのような値を取るのだろうか。おおよその値だけでも把握したい。そこで、信頼区間を求め、おおよその確率(95%など)で真のパラメータが含まれている区間を確認する。OLSEの漸近的性質と中心極限定理により、サンプルサイズが十分に大きいとき、先述の統計量 t は標準正規分布に近づくことが知られている(西山ほか,2019)。
そのため、標準正規分布に基づく信頼区間の推定を応用できる。信頼係数を \(\small \alpha\) とすると、以下の確率と区間の対応関係を得る。
\[ P\left(\left|\frac{\hat{\beta}-\beta}{se(\hat{\beta})}\right|\leq z_{\alpha/2}\right)=1-\alpha \]
そして、上記を \(\small \beta\) に関する不等式に変換すると、以下の信頼区間を得る。
\[ P(\hat{\beta}-se(\hat{\beta})\cdot z_{\alpha/2}\leq\beta\leq\hat{\beta}+se(\hat{\beta})\cdot z_{\alpha/2})=1-\alpha \]
したがって、\(\small [\hat{\beta}\pm se(\hat{\beta})\cdot z_{\alpha/2}]\) という観察可能な情報によって信頼区間が推定できる。Rによって信頼区間を得るには、回帰分析の結果に対して、confint() 関数を用いる(デフォルトで95%信頼係数が設定されている)。例えば、先程の reg1の結果を用いて、99%信頼区間を求めると、以下のような結果を得る。
## 0.5 % 99.5 %
## (Intercept) -210798.52845 255026.48944
## emp 51.43362 64.84799したがって、emp の99%信頼区間が [51.4, 64.8] であることがわかった。すなわち、企業の従業員が一名多いと、売上高が 51から64 百万円高くなりそうだと解釈できる。一方で、(Intercept) の信頼区間には0を含んでいることが伺える。なお、confint() 関数によって計算される信頼区間の計算では上述の通り正規分布が仮定されており、詳しくはヘルプ(?confint)で確認できる。