11.5 (おまけ)主成分分析との違い
因子分析とよく対比される手法として主成分分析(Principal component analysis)がある。主成分分析は、複数の変数間の類似性を分析し、これらの変数をできるだけ少ない数の合成変数(主成分)にまとめることを目的とした分析手法である。そのため、この主成分はできるだけ高い寄与率を持つことが求められる。主成分分析は、変数が多いとき情報の損失を最小限に押さえながらできるだけ少ない(理想的にはひとつの)主成分に縮約する方法であるといえる。一方で因子分析は、観測変数を「メリハリのある分かれ方(単純構造)」にするように因子数の決定や負荷量の計算が行われる(分寺, 2022, p.55)。主成分の計算方法は本資料では省略するが、興味のある人は田中・脇本(1998)や、渡辺(2017)を参考にしてほしい。
主成分分析のモデルは、図11.13 のように示される。因子分析のパス図(11.3)と比べると、矢印の向きに違いがあることがわかる。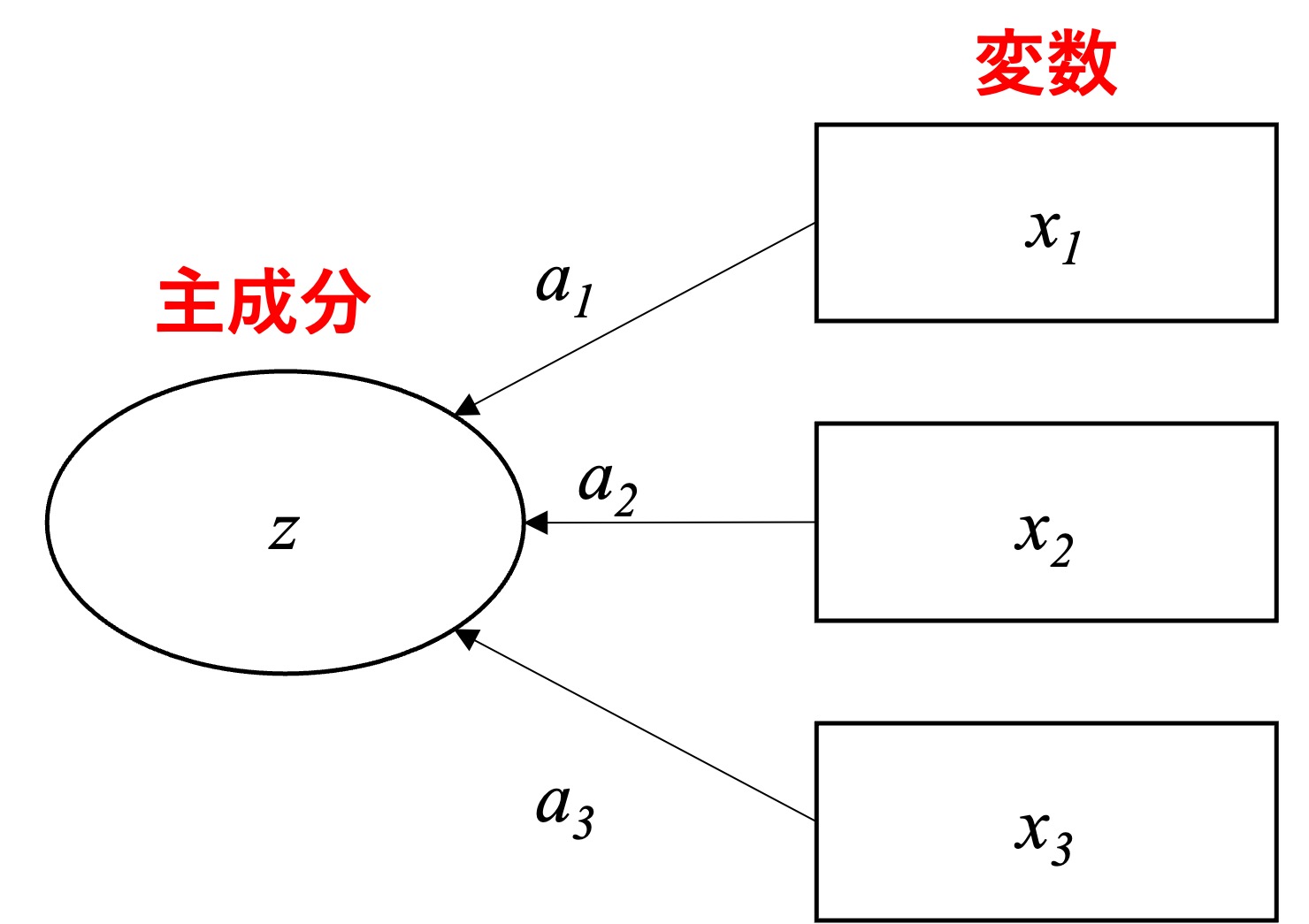
Figure 11.13: 主成分分析モデル
同様に、主成分モデルを式で表すと以下のようになる:
\[ z_i=b_1x_{1i}+b_2x_{2i}+b_3x_{3i} \]
主成分分析と因子分析とではモデル化のコンセプトが異なる。主成分分析では、変数から主成分を導き出すという想定でモデル化されていることが伺える。一方で因子分析はあくまで背後にある潜在因子が観測変数を規定すると想定している。そのため因子分析を用いる場合には、因子と変数の前後関係が想定できるような現象を捉えたデータにのみ有効である。また、誤差項(独自因子)を含まないということも主成分分析モデルの特徴である。
主成分分析は計算方法においても因子分析とは異なる点を有する。結論から述べると、主成分分析は因子分析の特殊形と考えられる(渡辺, 2017 参照)。計算上では、主成分分析は因子分析における主因子法というアプローチの特殊な場合と位置づけられる。主因子法とは、ある制約のもとで、各因子が観測変数の分散を説明する寄与率を最大にするように因子を求める計算方法である。この方法では、共通性を最初に計算し、因子負荷量を算出、因子数を決定した後再度共通性を計算する。そして新しく得られた共通性をもとに再度因子負荷量を算出するというプロセスを繰り返す。計算における共通性の初期値は1や、重相関係数の2乗値、相関行列の行の相関の最大絶対値などが使われる。
これに対して主成分分析は、共通性初期値を1とし、繰り返し計算を行わない主因子法といえる。より細かく述べれば、主成分分析によって求められる主成分係数(上式の \(b_1, b_2, b_3\))は項目間分散共分散行列の固有ベクトルとして計算される一方で、因子負荷量は対角要素に共通性を代入した項目間相関行列の固有ベクトルに固有値の平方根を乗じたものだといえる(渡辺, 2017)。そのため、標準化された項目を用いた主成分分析によって得る主成分係数(項目間相関行列の固有ベクトル)に固有値の平方根を乗じると、対角要素を1とした項目間相関行列の因子負荷量(ただし、繰り返し計算は行わない)と等しくなる。
Rで主成分分析を行う際は、psych::pca() を用いる。ここで、11.3 節で用いた演習用データを用いて、主成分分析を実行し、それが、「項目間相関行列の固有ベクトルに固有値の平方根を乗じたもの」と等しくなるかを検討する。まず主成分分析を実行するが、デフォルトでは軸の回転を行ってしまうので、ここでは rotate = "none"とする。
factor_exdata3 <- factor_exdata %>%
select(-ID)
pca_res <- pca(factor_exdata3, nfactors = 2, rotate = "none")
pca_res## Principal Components Analysis
## Call: principal(r = r, nfactors = nfactors, residuals = residuals,
## rotate = rotate, n.obs = n.obs, covar = covar, scores = scores,
## missing = missing, impute = impute, oblique.scores = oblique.scores,
## method = method, use = use, cor = cor, correct = 0.5, weight = NULL)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 h2 u2 com
## V1 0.93 0.25 0.93 0.074 1.1
## V2 -0.30 0.80 0.72 0.277 1.3
## V3 0.94 0.13 0.89 0.106 1.0
## V4 -0.34 0.79 0.74 0.261 1.4
## V5 0.87 0.35 0.88 0.122 1.3
## V6 -0.18 0.87 0.79 0.210 1.1
##
## PC1 PC2
## SS loadings 2.73 2.22
## Proportion Var 0.46 0.37
## Cumulative Var 0.46 0.82
## Proportion Explained 0.55 0.45
## Cumulative Proportion 0.55 1.00
##
## Mean item complexity = 1.2
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.07
## with the empirical chi square 3.94 with prob < 0.41
##
## Fit based upon off diagonal values = 0.98続いて、項目間相関係数の固有ベクトルを計算し、それに固有値の平方根を乗じる。その結果、表11.5 は(PC2については符号は異なるものの)上記の主成分分析の結果と一致している事がわかる。
#データの相関行列から固有値と固有ベクトルを抽出
cor_ex <- cor(factor_exdata3)
eigen_list <- eigen(cor_ex)
#固有ベクトルについての情報をオブジェクトとして定義
pc1_eig <- eigen_list$vectors[, 1]
pc2_eig <- eigen_list$vectors[, 2]
#固有ベクトルに、固有値の平方根を乗じる
PC1 <- pc1_eig* sqrt(eigen_list$values[1])
PC2 <- pc2_eig* sqrt(eigen_list$values[2])
knitr::kable(data.frame(cbind(PC1,PC2)), caption="計算結果")| PC1 | PC2 |
|---|---|
| 0.9283425 | -0.2532285 |
| -0.3005297 | -0.7952496 |
| 0.9361812 | -0.1308894 |
| -0.3415817 | -0.7889663 |
| 0.8687553 | -0.3507939 |
| -0.1766389 | -0.8711581 |