8.3 重回帰モデル1
ここまでは、回帰分析の概要や係数の検定・推定について説明した。回帰分析を実行することで得る情報は前節の内容がほとんどなのだが、モデルの特定化に関して、もう一つ重要な点が存在する。それが本節で扱う重回帰モデル(multiple regression model)の採用である。重回帰モデルとは、二つ以上の説明変数を含む回帰モデルのことである。一方で、前節で扱ったような説明変数が一つの回帰モデルのことを単回帰(simple regression model)という。回帰分析を用いた研究を行う際には、基本的に単回帰分析ではなく、重回帰分析を実行することが好ましい。通常の分析においては、ある被説明変数に対して考慮すべき説明変数は一つだけではなく、複数の説明変数を考慮すべき状況が多い。しかし、分析に不慣れ学生においては、複数の説明変数に関心がある場合であっても、複数の単回帰モデルを分析することで、それぞれの変数についての分析結果を得ようとすることが散見される(例えば、三つの説明変数の影響を捉えるために単回帰モデルを三本分析する等)。しかしながら本書は、基本的にはこのような分析アプローチは好ましくなく、複数の説明変数を含めた一本の重回帰分析を実施すべきだと主張する。本節では、この主張の理由と、重回帰モデルの特徴・結果解釈について説明していく。
8.3.1 重回帰モデル概要
ある成果変数を説明するために、複数の説明変数が必要になることは、マーケティングリサーチにおいても珍しいことではない。例えば、ある製品のパフォーマンスを月次売上高で測るとする。マーケティング部門として、売上高に対してプロモーション施策がどれだけ貢献しているかを分析する際、プロモーションと売上高の関係を回帰分析で捉えるというアプローチが実現可能な分析方法として考えられる。しかしながら、売上高を説明する変数として、プロモーションだけで十分だろうか。マーケティング変数に着目するだけでも、価格や製品品質、流通網など、異なる変数が売上に関係していることが考えられる。例えば、一見プロモーションによる効果のような結果を得たとしても、実際には同時期に実行していたディスカウント(価格)の影響であり、プロモーションそのものにはあまり効果がないかもしれない。そのため、他の要素の影響を排除した上での純粋なプロモーション効果を明らかにすることは務的有意義な研究課題となりうる。そしてこのような研究課題に対応する分析方法が、重回帰分析である。本節ではまず、重回帰モデルに関する特徴を整理する。
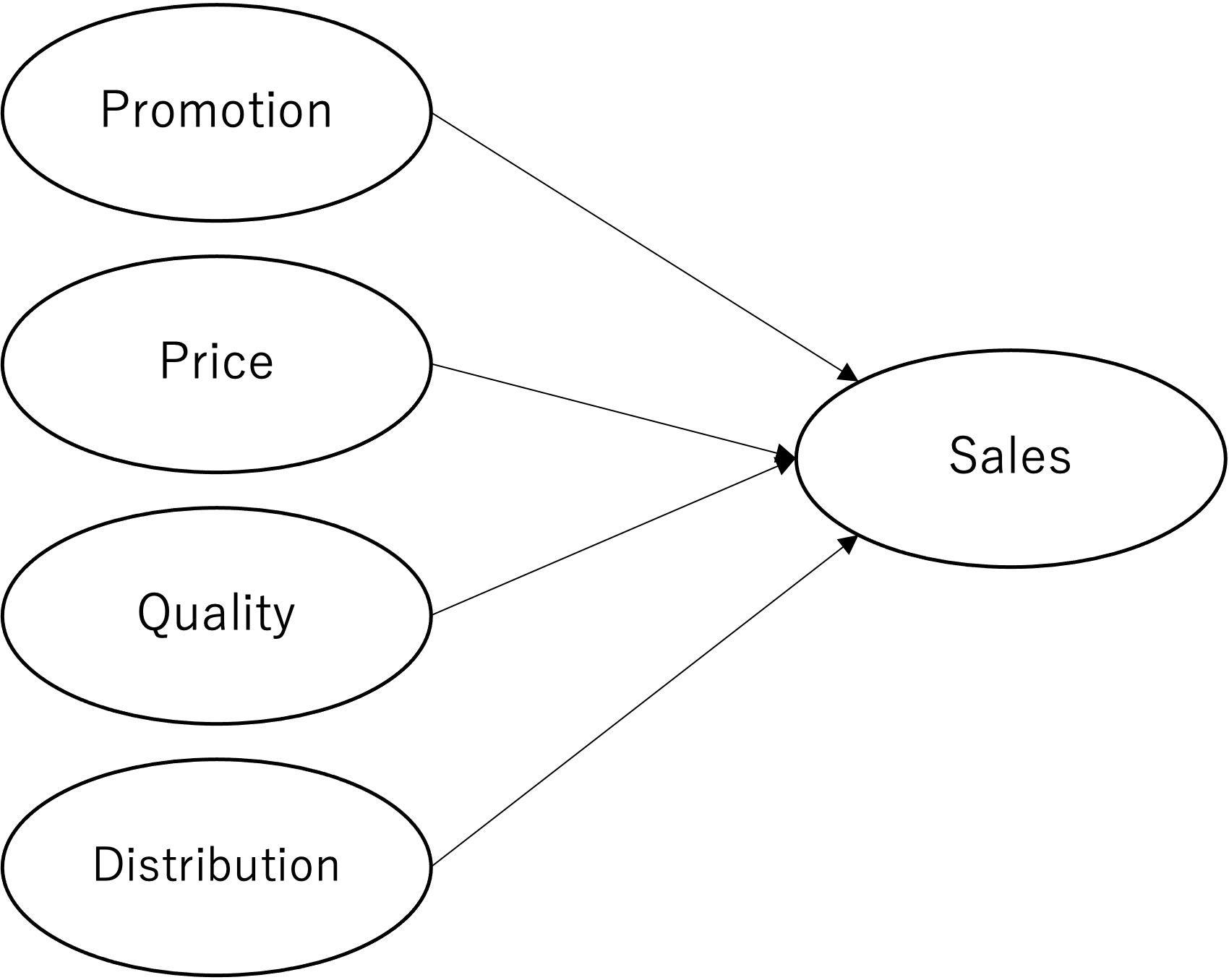
重回帰分析においても単回帰同様、回帰モデルを記述する。k 個の説明変数を含む重回帰モデルは、以下のように示される。
\[ y_i = \beta_0+\beta_1x_{1i}+\beta_2x_{2i}+...+\beta_kx_{ki}+u_i \]
論文やレポート内に重回帰モデルを記載する際にも、多くの場合上記の誤差項を含む理論モデルを用いる。
以下ではまず、重回帰モデルの係数、予測値や、残差に関する性質について説明する。係数の推定は、以下のような行列モデルで捉えることで、単回帰モデルと同様OLSで求められることができる(詳細は省略)。
\[ Y = X'\beta + u \]
\[ \hat{\beta}=(X'X)^{-1}X'Y \] 重回帰分析を実行すると、各説明変数に対応する係数が推定される。各OLSE(\(\small \hat{\beta}\))は 未知パラメータ(\(\small \beta\))の不偏推定量である。また、それらの検定や区間推定では、各変数に対応する係数の検定・推定を個別に行う。OLS推定に関わる残差と予測値はそれぞれ以下のように意義される。
予測値: \[ \hat{y}_i = \hat{\beta}_0+\hat{\beta}_1x_{1i}+\hat{\beta}_2x_{2i}+...+\hat{\beta}_kx_{ki} \]
残差: \[ \hat{u}_i=y_i-\hat{y}_i =y-( \hat{\beta}_0+\hat{\beta}_1x_{1i}+\hat{\beta}_2x_{2i}+...+\hat{\beta}_kx_{ki}) \] そして、残差は以下の \(k+1\) 個の制約を満たす。
\(\sum_{i=1}^n\hat{u}_i=0\)
\(\sum_{i=1}^n x_{1i}\hat{u}_i=0,~\sum_{i=1}^nx_{2i}\hat{u}_i=0...,~\sum_{i=1}^nx_{ki}\hat{u}_i=0\)
そのため、重回帰モデルの残差の自由度は \(n-(k+1)\) となる。
8.3.2 重回帰分析におけるモデル適合度
単回帰モデルにおけるモデル適合度指標として前節では決定係数を紹介した。しかしながら、この指標は致命的な欠陥を有している。それは、モデルに含む説明変数の数が増えると決定係数も上昇する(より正確には、説明変数の数に対して非減少)ということである。つまり、被説名変数と全く関係ない変数をモデルに加えても、決定係数は上昇し、そのモデルの説明力が高いという結論に至ってしまう。そのため、通常の決定係数から説名変数の数を調整した指標である調整済み決定係数(Adjusted R-squared: \(\bar{R}^2\))を用いて適合度を検討する。この指標は、以下のように定義される。
\[ \bar{R}^2= 1 - \left(\frac{\sum(y_i-\hat{y}_i)}{n-k-1}\cdot \frac{n-1}{\sum(y_i-\bar{y})}\right) \]
モデルの適合度を考えるもう一つの分析として、Rの分析結果で出力されていたF検定について説明する。回帰分析の結果として必ず出力されるF検定は、重回帰モデルにおける\(\small \beta_0\)(定数項) 以外の係数が全て0であるか否かをチェックする検定である。この検定では、k個の説明変数を含む回帰モデル(\(\small y_i = \beta_0+\beta_1x_{1i}+\beta_2x_{2i}+...+\beta_kx_{ki}+u_i\))に対して(これをフルモデルと呼ぶ)、以下のような帰無仮説と対立仮説を用いた検定を行う。
\[ H_0:~\beta_1=...=\beta_k=0,~H_1:\text{少なくともどれか一つの係数は0ではない} \] 帰無仮説が正しいと仮定した場合、重回帰モデルは以下のようになり、この定数項のみのモデルをモデル0と呼ぶ。
\[ y_i = \beta_0+e_i \]
そして、フルモデルとモデル0の残差平方和の比を取った統計量は、帰無仮説が正しいときには自由度(\(k,~n-k-1\))の F分布に従うことが知られている。この性質を活かし、回帰分析においては自由度(\(k,~n-k-1\))のF分布を前提とした統計検定を行い、それをF検定(F-test)と呼ぶ。回帰分析結果にて出力される F-statistic:は、この検定統計量の実現値である。なお、この検定の検定統計量は、以下のように示される。
フルモデルとモデル0の残差平方和(\(SSR_1\)と\(SSR_0\))をそれぞれ以下のように定義する。
\(SSR_1=\sum\hat{u}^2_i=\sum\left[y-( \hat{\beta}_0+\hat{\beta}_1x_{1i}+\hat{\beta}_2x_{2i}+...+\hat{\beta}_kx_{ki})\right]^2\)
\(SSR_0=\sum\hat{e}^2_i=\sum(y_i-\bar{y})^2\)
そして、以下の統計量 F は帰無仮説が正しければ、自由度(\(k,~n-k-1\))の F分布に従うことが知られているため、これを検定統計量として用いて検定を行う。
\[ F=\frac{(SSR_0-SSR_1)/k}{SSR_1/(n-k-1)}=\frac{SSR_0-SSR_1}{SSR_1}\cdot\frac{n-k-1}{k} \]