12.3 PSMに関する既存研究

12.3.1 受容価格に関する知見

本節ではまず、PSMのもとになっている、受容価格帯に基づく価格分析として Gabor and Grager (1966) について紹介する。PSMは主にマーケティング実務上での活用を前提提示された手法であり、学術研究分野ではあまり言及されることはない。しかしながら、PSMは前節で述べた受容価格帯と内的参照価格に関する学術的知見に基づき提唱されたという経緯がある。

受容価格帯に関する知見としては、Gabor and Granger (1966) による購買反応曲線（Buy Response Curve；以下、BRC）の知見が活かされている。本節では、この論文の知見を簡単に紹介する。詳細について関心がある場合にはぜひ論文を読んで見てほしい。逆に、PSMに関する理論的背景に関心がない場合には、「実務的に広く使われているPSMにも、学術的な蓄積がある」ということさえ頭に留めてくれれば、そのまま次節へ進んでもらっても構わない。

Gabor and Granger (1966)では価格に対する需要量の変化ではなく、ある価格においてその製品が購買される可能性（Plausibility）について捉えた議論を展開している。この研究では受容価格の上限と下限に着目し、ある価格Pにおいて、消費者がそれを安すぎると感じる確率を\(L(P)\)、価格Pにおいて、消費者がそれを高すぎると感じる確率を \(H(P)\) とした（ただし、\(0\leq L(P)\leq1\)かつ\(0\leq H(P)\leq1\)）。これらの確率は、下図で示されるように、\(H(P)\)が単調増加である一方で、\(L(P)\) は単調減少であり、\(L(P)\) ではなく \(1-L(P)\) が累積分布関数として捉えられる。

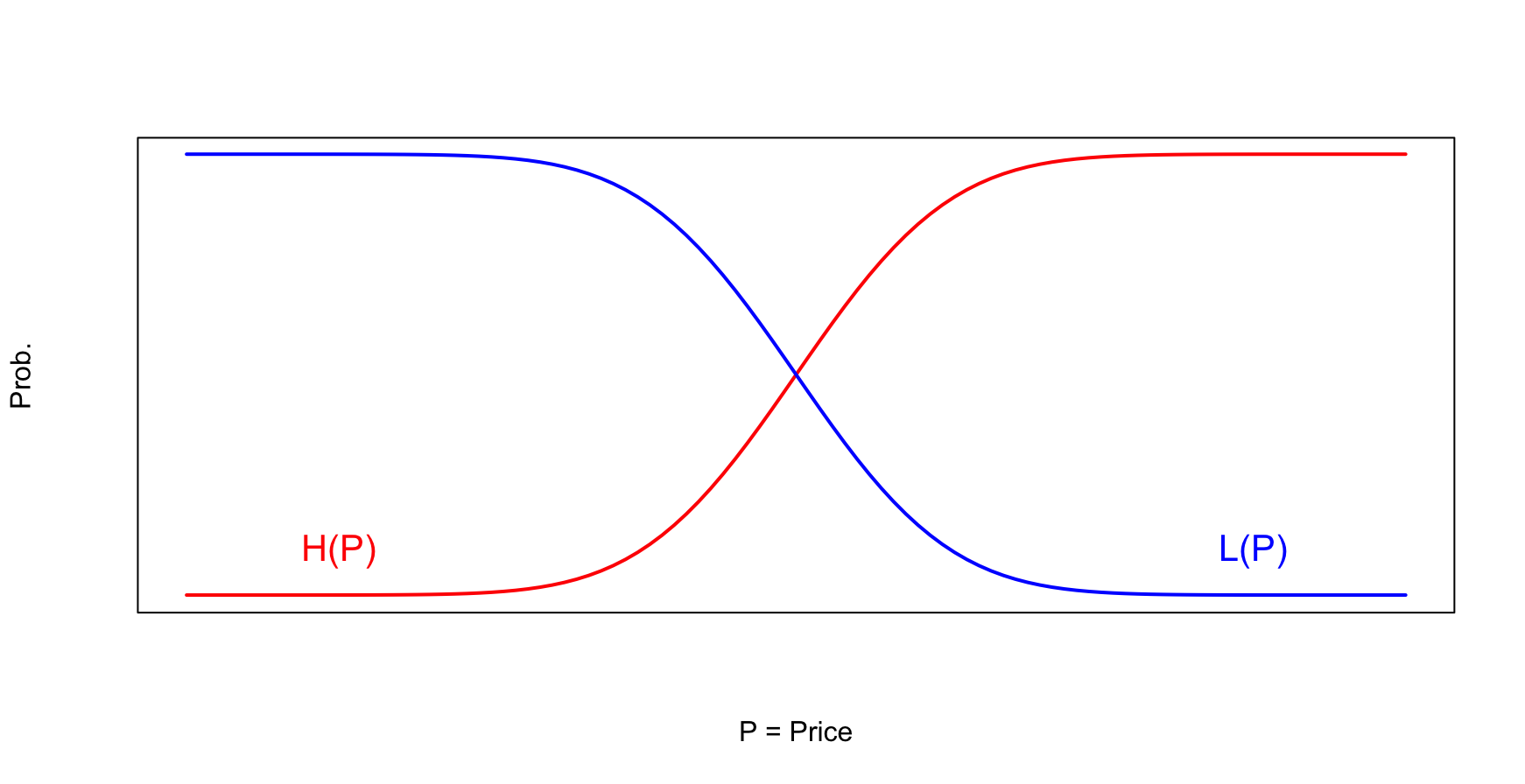
Figure 12.2: L(P)とH(P)

これらを用いて、価格Pが消費者の受容価格範囲に入っている確率を \(B(P) = 1- L(P) - H(P)\) と定義した。ただし、\(H(P)\) と \(L(P)\) はすべての \(P\) に対して微分可能であり、\(l(P)=dL(P)/dP\)、\(h(P)=dH(P)/dP\)とする。\(B(P)\)は、ある価格Pを消費者が高すぎるとも安すぎるとも感じない確率と言い換えることができ、これを購買反応曲線（BRC）と呼んだ。BRCの形状は以下のように示すことができる。この形状から、\(P'\) という価格水準を基準とし、それより高いないし低い価格において、購買される可能性が低くなることが予想される。

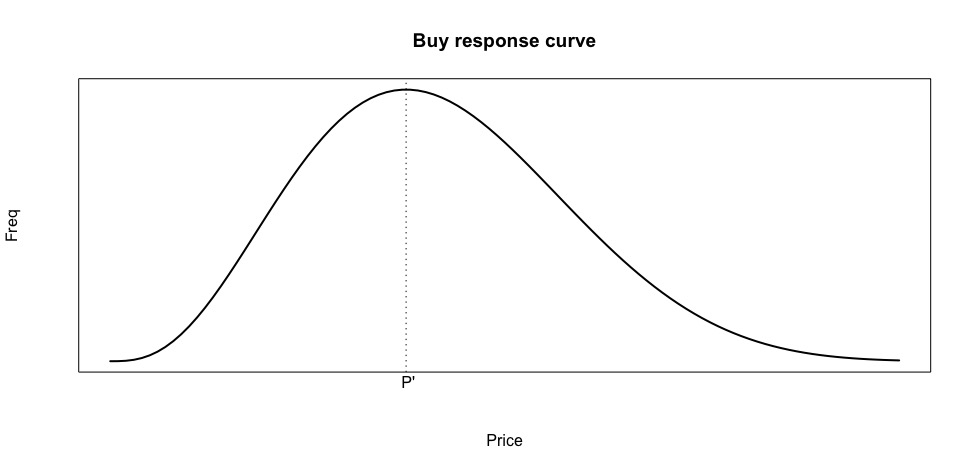
Figure 12.3: 購買反応曲線

Gabor and Granger (1966)は思いつきや恣意的に曲線の形状を決めたのではなく、いくつかの仮説に基づき、BRCの形状について議論を発展させた。これが、彼らの研究の一番の理論的貢献である。特に、ここで想定されている仮説を確認することで、BRCの議論においてどのような消費者像が想定されているのかについて理解が可能になる。

例えば論文内では、１つ目の仮説（H1）として、先述の \(l(P)\) と \(h(P)\) をそれぞれ、低すぎ頻度関数と高すぎ頻度関数と呼び、これらが対数正規の密度関数に従うという仮説を述べた。つまり、\(p = logP\) としたとき、\(l(p)\) と \(h(p)\) は正規分布に従うと考えられる。ここでは、Weber-Fechner law という、「ある刺激とそれに対する個人の知覚の関係は対数的である」とする理論に基づき、対数線形を用いた形状を仮定している。言い換えると、Gabor and Granger (1966) によるBRCは、価格の増加という刺激を感覚（お得感や割高感等）として知覚する消費者像を想定したモデルだと解釈できる。

仮説2（H2）では、ある価格と消費者グループにおいては、\(l(p)\) と \(h(p)\) の標準偏差は近似的にほぼ等しいと述べた。詳細は割愛するが、H1とH2を含む計4つの仮説と整合的な結果を得ることで、BRCの形状についての知見を獲得した。\(1-L(p)\) と \(H(p)\) が正規の確率分布関数に従うとするならば、\(B(p) = 1- L(p) - H(p)\) の理論的な形状も推察できる。ただし、\(B(p)\) 自体は確率密度関数ではない。Gabor and Granger (1966) では、\(m_1\) と \(m_2\) をそれぞれ、\(l(p)\) と \(h(p)\) の期待値とし、\(b(p)=B(p)/(m_2-m_1)\) を確率密度関数と捉えた。単純化のために H2 を仮定すると、\(b(p)\) は \((m_1+m_2)/2\) を中心に左右対称である。これらの仮説および議論のもと、\(l(p)\)、\(h(p)\)と、\(b(p)\) は以下のように図示できる。このように、Gabor and Granger (1966)は、いくつかの仮定を満たすような状況では、消費者の価格に対する反応を数量的に分析することが可能になることを示した。

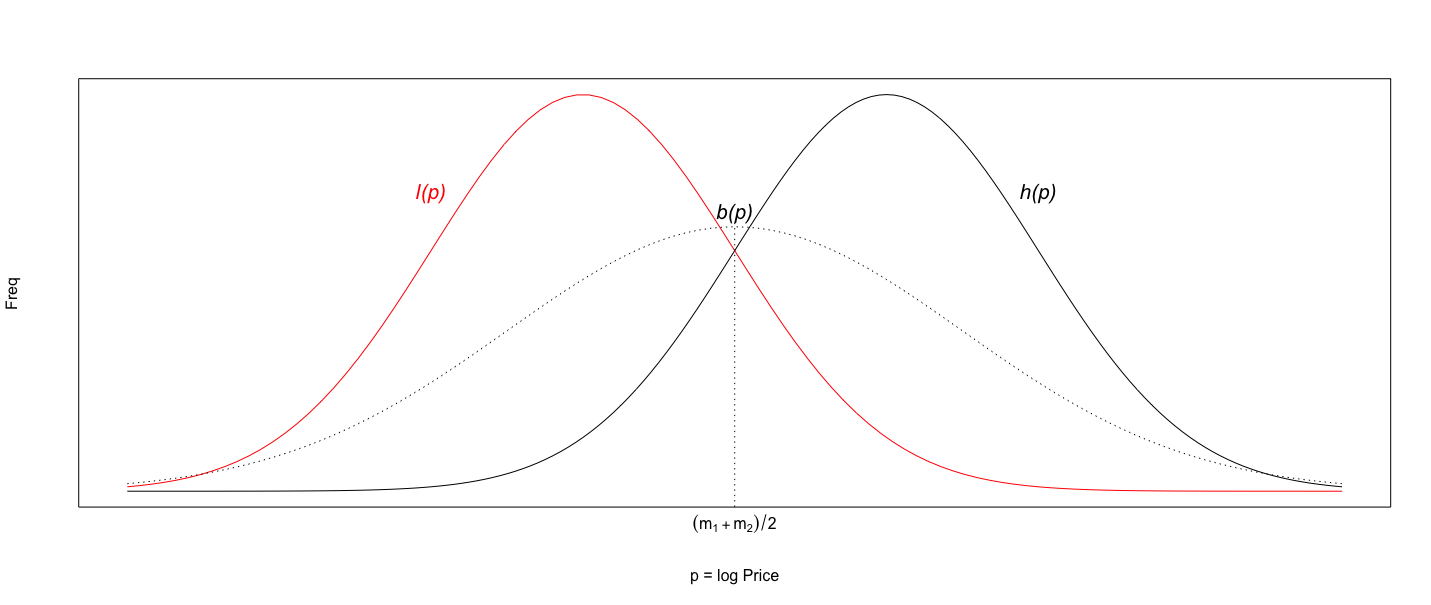
Figure 12.4: 購買反応密度関数

12.3.2 内的参照価格に関する知見

受容価格に関するBRCに加え、内的参照価格についての知見もPSMには重要である。詳しくは兼子（2014）を参照してほしいが、内的参照価格にも幅が存在すると考えられる。つまり、受容価格帯内において安いか高いかを知覚する価格は特定の水準だけでなく、価格幅として構成されると考えられる。ある製品の価格が消費者にとって高いと感じる価格帯よりも低く、安いと感じる価格帯よりも高い価格幅に含まれている場合、その価格は「安くも高くもない」価格として知覚される。言い換えると、この安くも高くもない価格幅に基づき、その上限よりも高い価格については高いと感じ、下限よりも低い価格については安いと感じると考えられる。以下では、兼子（2014）を参考に、受容価格帯（\(P_4-P_1\)）と内的参照価格帯（\(P_3-P_2\)）を図示する。

Figure 12.5: 内的参照価格帯

上図における、\(P_1\) を安すぎる価格の上限、\(P_2\) を安いと感じる価格の上限、\(P_3\)を高いと感じる価格の下限、\(P_4\) を高すぎる価格の下限と考える。そのため、\(P_1\) より低い価格や、\(P_4\) より高い価格の場合には消費者は購買しないと仮定する。一方で、\(P_2-P_1\) の範囲では、安いと感じるが買うと考えられるし、\(P_4-P_3\) の範囲では高いと感じるが買うと考えられる。このように、受容価格帯と内的参照価格帯の関係を捉えることで、「買う買わない」に加えた消費者の価格に対する感じ方も捉えた含意を得ることができる。