9.4 対数線形

ここまでの回帰モデルの特定化では、一次関数を利用していた。しかしながら、以下の図のように傾きの大きさが途中で変化するような非線形の関係には一次関数のモデルは上手くフィットしない。

非線形例
非線形例

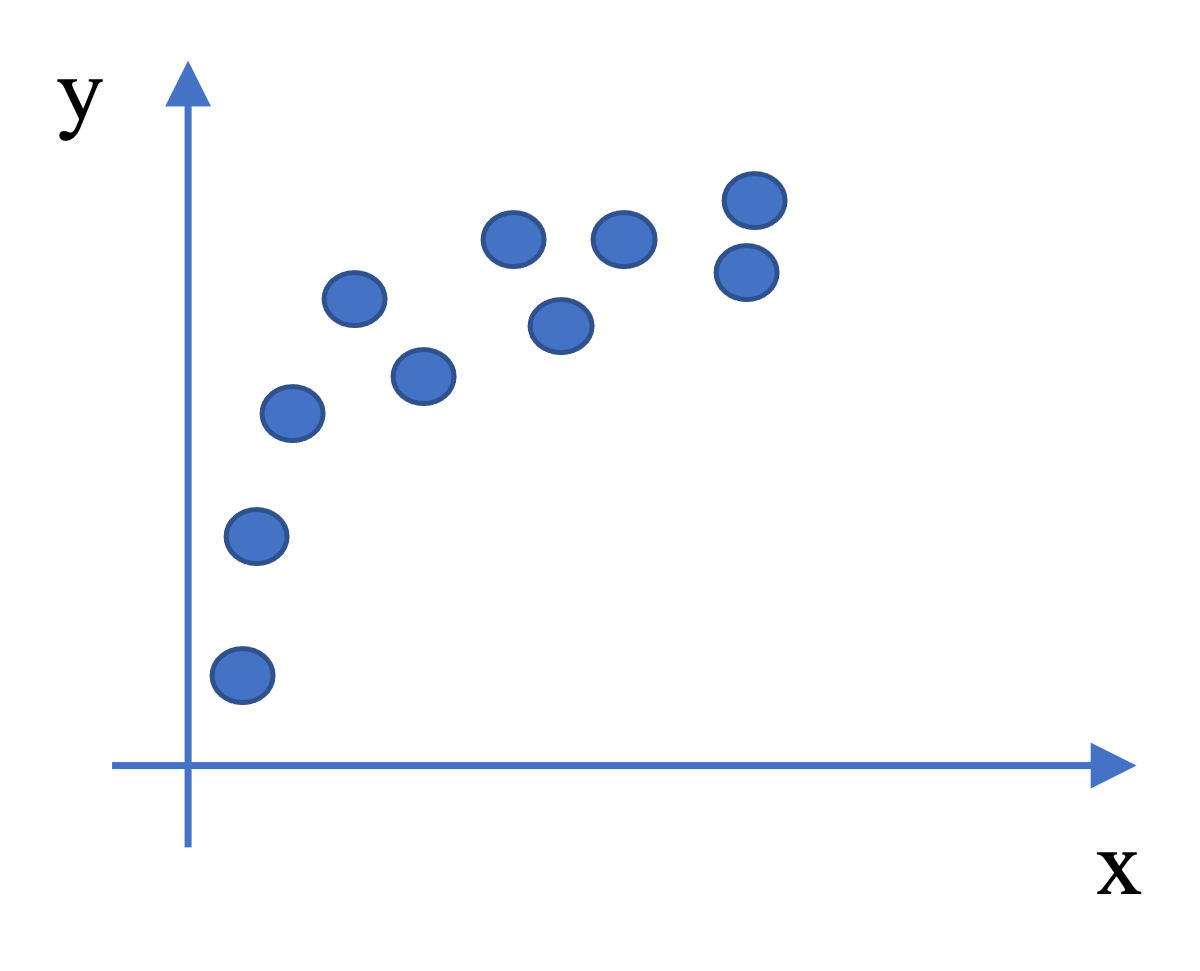
非線形の関係として例えば、以下のような関数形がある。

\[ Y=AL^\alpha K^\beta \]

ここで、Yは生産量、Lは労働投入量、K は資産を仮定すると、上記の式は、経営学分野にも応用される、経済学におけるコブダグラス型の生産関数として知られている。しかしながら、このような関数をそのまま線形回帰分析に当てはめることはできない。そこで、右辺と左辺両側の変数に対して、自然対数を用いた変数変換を行うことで、回帰分析で推定可能なモデルを構築する。このような変換された説明変数（例、\(\small \ln K_i\)）を用いる定式化であれば、推定される係数については線形の形で扱うことができる。対数による変数変換を伴う線形回帰モデルは、一般に対数線形モデルと呼ばれる。

\[ \ln Y_i = \ln A + \alpha\ln K_i+\beta\ln L_i + u_i \]

このような回帰式をR上で構築することは難しくない。lm() 関数内のモデル定式化において、log() を用いれば良い。例えば、上の式を firmdata19 に当てはめて、Yを売上、Lを人件費、K を有形固定資産とおいて、以下のようにモデルを推定してみる14。

fit_prod <- lm(log(sales) ~ log(labor_cost) + log(ppent), data = firmdata19)

summary(fit_prod)
## 
## Call:
## lm(formula = log(sales) ~ log(labor_cost) + log(ppent), data = firmdata19)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.4058 -0.3725 -0.0108  0.3870  1.6627 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)      3.17985    0.31763   10.01   <2e-16 ***
## log(labor_cost)  0.53793    0.03684   14.60   <2e-16 ***
## log(ppent)       0.34438    0.02797   12.31   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5176 on 144 degrees of freedom
## Multiple R-squared:  0.8735, Adjusted R-squared:  0.8718 
## F-statistic: 497.2 on 2 and 144 DF,  p-value: < 2.2e-16

このような対数線形モデルでは、これまでのような一次関数モデルとは異なる係数の解釈を行う必要がある。両側対数の回帰モデルにおける回帰係数は、「弾力性」を表している。つまり係数は、説明変数が 1% 増加したとき、被説明変数が何%変化するか（変化率）を表している。また、この係数解釈の特徴から、マーケティング分野においても対数線形モデルはよく用いられる。具体的には、対数線形モデルによって需要の価格弾力性（価格が1%増えたときに、需要量が何%減るか）を分析することができる。

需要の価格弾力性（\(\eta\): イータ）は、消費者による価格感度を捉える指標である。通常、他の要素を一定とした場合、価格が低いと需要量は上がる。では、どの程度価格の低下が需要量に影響を与えるのかという問いは、実務的にも学術的にも重要になる。その際に、単位に依存しない価格感度の尺度として最も広く使われているものが、需要の価格弾力性である。また弾力性は、1を重要な閾値として実務的に重要な含意を与える。弾力性値に応じた含意は以下のように整理することができる。

  • \(\small \eta= 1\) の場合:

    • 価格が1%下がった時に需要量が1%上がることを意味する。価格と需要の変化率がちょうど釣り合った状態。

  • \(\small \eta > 1\) の場合:

    • 価格の上昇によって需要量が著しく減る（価格に敏感に反応する）。
    • 価格の上昇によって売上を損ねる（需要量の損失が価格上昇の便益を上回っている） 。

  • \(\small \eta < 1\) の場合:

    • 価格の上昇によって需要量があまり減らない（価格に敏感に反応しない）
    • 価格の上昇によって売上が伸びる（価格上昇の便益が需要量の損失を上回っている） 。以下では、対数線形モデルと需要の価格弾力性との関係に関する補足的な説明を追加している。

9.4.1 需要の価格弾力性追加説明

ここでは、需要の価格弾力性についてもう少し詳細な説明を加える。興味のない場合は読み飛ばしてもらって構わない。需要の価格弾力性は、需要量（q）と価格（p）とし、以下の \(\eta\)のように定義できる。

\[ \eta=-\frac{dq}{dp}\times \frac{p}{q} \]

この価格弾力性の定義に基づき、なぜ１が重要な閾値になるのかを説明する。 価格の変化による売上の変化\(dpq/dp\) の関係を変形することで \(\small \eta\) について以下を得る。

\[ \eta=\frac{dpq}{dp}=-p\cdot\frac{dpq}{dp}+p=q\left[1-\left(-\frac{dq}{dp}\cdot\frac{p}{q}\right)\right]=q(1-\eta) \]

そのため、\(\small \eta\) が１より小さい時、価格の増加による売上の変化が正（\(dpq/dp>0\)）であることが伺える。

9.4.2 対数線形の推定と検定

ここで、需要の価格弾力性に関する分析を実行するために、“price_data.csv” という人工データを用いる。このデータは製品の価格と需要量の情報を含んでいる。以下のようにデータを読み込み、分析を実行してほしい。

price <- readr::read_csv("data/price_data.csv")

fit_q <- lm(log(q) ~ log(p), data = price)
summary(fit_q)
## 
## Call:
## lm(formula = log(q) ~ log(p), data = price)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.11220 -0.13668  0.02804  0.16166  0.51039 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  9.47781    0.08135   116.5   <2e-16 ***
## log(p)      -0.18008    0.01354   -13.3   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.2309 on 998 degrees of freedom
## Multiple R-squared:  0.1506, Adjusted R-squared:  0.1497 
## F-statistic: 176.9 on 1 and 998 DF,  p-value: < 2.2e-16

分析の結果、log(p) の係数は負に有意であった。しかしここで、デフォルトで出力される検定結果の「帰無仮説」を思い出して欲しい。これは、係数が0か否かの検定を行っている。しかしながら、我々は係数が 1 より高いか、低いかに興味がある。そのため、\(\small H_0:\beta = 1\)という帰無仮説による検定を採用すべきである。このような検定の実行には、色々とやり方はあるが、本書では carというパッケージのlinearHypothesis() 関数 を用いる方法を紹介する。まず、以下のようにパッケージをインストールして欲しい。

install.packages("car")

そして、linearHypothesis()において、参照する分析結果と、着目する変数（の係数）とその値について入力することで、検定を行う。

library(car)
## Loading required package: carData
## 
## Attaching package: 'car'
## The following object is masked from 'package:dplyr':
## 
##     recode
## The following object is masked from 'package:purrr':
## 
##     some
linearHypothesis(fit_q, c("log(p) = -1")) 
## Linear hypothesis test
## 
## Hypothesis:
## log(p) = - 1
## 
## Model 1: restricted model
## Model 2: log(q) ~ log(p)
## 
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1    999 248.811                                  
## 2    998  53.225  1    195.59 3667.3 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

検定の結果、fit.q による係数の推定値は、有意に -1 とは異なることがわかった。つまり、弾力性は 1 より低く、非弾力的である（価格にあまり敏感でない）ことが伺えた。なお、一つの説名変数の有意性検定にF検定を用いる場合のF分布は対応するt分布の二乗値に等しい。そのため、car による検定では、F値を返しているが、それ自体に問題はない。

最後に、回帰モデルにおいて対数化を右辺（説明変数）と左辺（被説明変数）のどちらに適用するかによって、係数の解釈が変わることを説明する。モデルの特定化と係数解釈の対応関係は、以下のように整理できる。

  • 両側対数（\(\ln y_i = \alpha + \beta\ln x_i + u_i\)）:
    • \(\beta\) は x が 1%変化したときの y の変化率を表している。
  • 被説明変数のみ対数（\(\ln y_i = \alpha + \beta x_i + u_i\)）:
    • \(\beta\) は x が 1単位変化したときの y の変化率を表している。
  • 説明変数のみ対数（\(y_i = \alpha + \beta\ln x_i + u_i\)）:
    • \(\beta\) は x が 1%変化したときの y の変化量を表している。

  1. なお、実際に研究において生産関数を推定する場合には、変数の特定化に関して、先行研究に基づきより慎重に検討する必要があるため注意して欲しい↩︎