12.5 集計方法に関する注意点

これまで紹介したPSMアプローチは、Westendorp (1976) によって提唱された方式であるが、、Newton et al. (1993) によって提唱された別のアプローチも広く採用されている。Newton et al. (1993) による方式（NMS型）でも、これまで説明した方式と同様の4つの質問を用いて最適価格、無差別価格、最高価格、最低価格を提示する。しかしながら、NMS型においては「高いと感じる」と「安いと感じる」消費者の比率の余事象は取らずに分析を行う。NMS型は広く用いられているものの、Newton et al. (1993) が誤った方法を紹介したことを起点に広まったとされている（兼子，2014）。

NMS型の PSM を用いると、最適価格と無差別価格は Westendorp 型の方式と等しい結果を得るが、最低価格と最高価格については異なる結果を得る。どちらの数値が正しいのかという点については議論があるものの、NMSは各曲線の交点についての論理的意味が見出しにくいという欠点を有している（兼子，2014）。

NMS型の考え方を簡易的に図示化する。安いおよび高いと感じる曲線を 1 (もしくは100%) から引く形で反転させない場合、最低価格（\(\underline{P}\)）は「高い」曲線（青い破線）と「安すぎる」曲線（赤い実線）との交点で求められる。これは、先述の図12.5 で示されている \(P_4-P_2\) の範囲に感じている回答者が多くなる価格を表している。 同様に、最高価格（\(\bar{P}\)）は安い曲線（赤い破線）と高すぎる曲線（青い実線）の交点で求められる。これは、\(P_3-P_1\) の範囲に感じている回答者が多くなる価格を表している。これらのことから、NMS型では、最高価格と最低価格の解釈が困難になると考えられる（兼子，2014）。NMS型でも前節までに説明したものと似た結果を得ることはできるのだが、その結果が既存の価格概念と整合的かつ直感的かという点に関して、問題を有している。

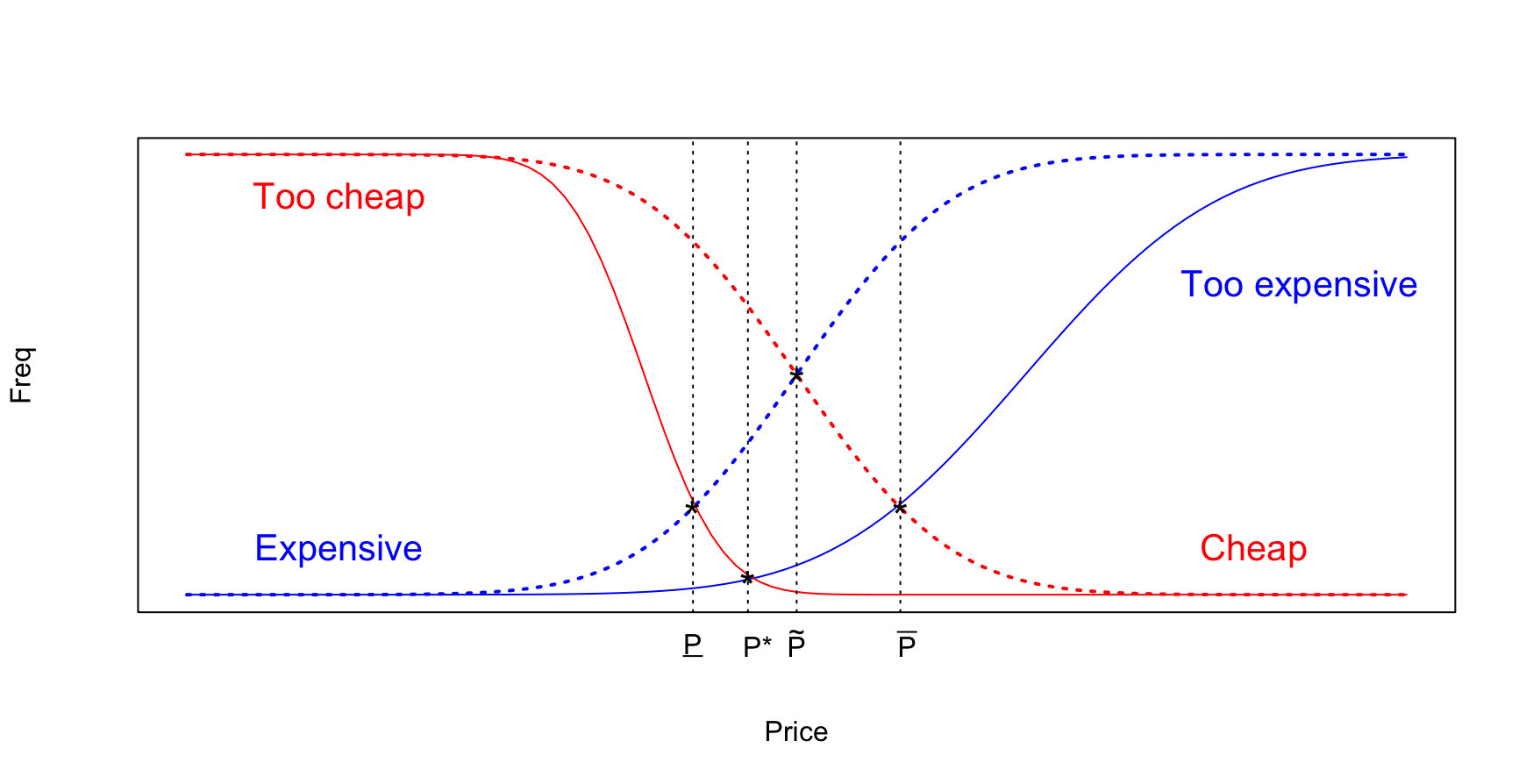
Figure 12.7: NMS型概要図

オンライン上では、NMS型のPSMを紹介している記事も散見される。実務的にもNMS型の方法を用いる場合もあるが、PSMの背後にある受容価格と内的参照価格に関する理論的基盤を鑑みると、Westendorp (1976) 方式のPSMアプローチのほうが、より実務的な含意を得やすい明示的な方法であると考えられる。PSMは使用の容易さから広く用いられているアプローチではあるが、本資料を読んだ学生においては、その背後に想定されている「受容価格」と「内的参照価格」という価格概念を理解したうえで活用してほしい。