9.1 ダミー変数
本節では、説明変数としてカテゴリ変数を用いる場合の方法と、その結果の解釈について説明する。マーケティング領域の研究においては、あるカテゴリに属することが成果変数にどのような影響を与えるのかに関心を持つことも多い。そのような場合には、「ダミー変数」と呼ばれる形にカテゴリ変数を定義し、分析することが多い。ダミー変数とは、特定のカテゴリに属するならば1を、それ以外なら0を取るような変数を指す。例えば、女性ならば1、それ以外の性別であれば0を取るようなダミー変数を、「女性ダミー」として扱うことができる。ダミー変数 D を用いた回帰モデルは以下の様に表すことができる、
\[ y_i=\alpha+\beta x_i + \gamma D_i+u_i \] ただし、\(x_i\) は連続尺度の説明変数である。ダミー変数は取りうる値が1か0に限定されているため、y の条件付期待値は以下のように解釈できる。
\[ E(y_i|D_i=1)=\alpha+\beta x_i + \gamma \]
\[ E(y_i|D_i=0)=\alpha+\beta x_i \]
つまり、ダミー変数に対応する回帰係数はベースライン(\(D_i=0\))グループとの「切片の差」を表しているということがわかる。例えば、\(\small \alpha\)、\(\small \beta\)と、\(\small \gamma\)が正の値を取るような場合、上記のダミー変数の関係は以下の図のように示す事ができる。例えば、このダミー変数が女性ダミーであるならば、女性はその他の性別に比べて、y の値が相対的に高い、と解釈できる。
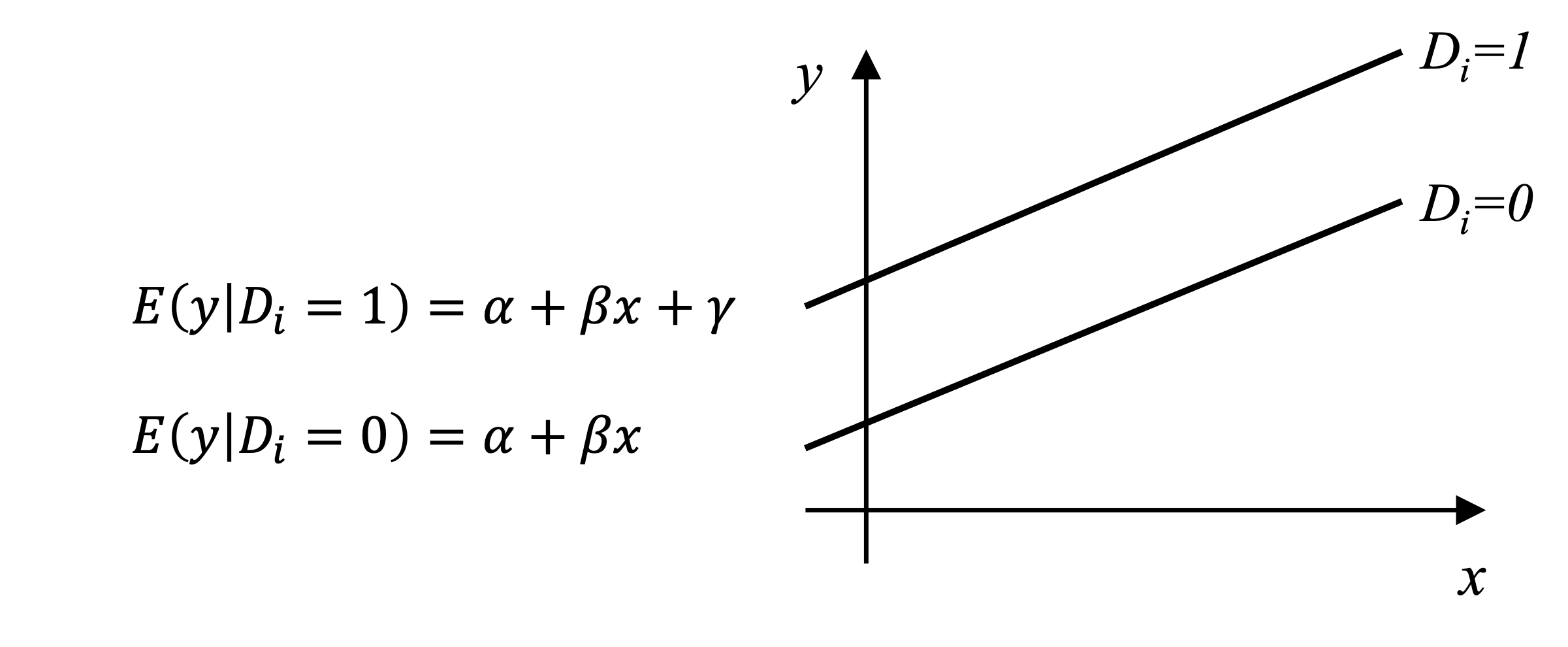
ダミー変数を説明変数に含む回帰分析をRで実行することはとても簡単である。lm() 関数内のモデル定義において、カテゴリ変数を含めば良いだけである。Characterという文字列情報のデータ型で示されているカテゴリ変数を用いると、自動でダミー変数化して、回帰分析を実行してくれる。
例えば、本章で使っている firmdata19 を使って分析を行ってみる。具体的には、営業利益率(営業利益/売上)が小売産業に属する企業とそれ以外で異なるかを分析する。しかし、データセット上にこの分類に対応するカテゴリー変数は存在しないため、以下のように、“Retail Stores, NEC” もしくは “Supermarket Chains” のどちらかに含まれる企業であれば1、それ以外であれば0を取るカテゴリー変数(format)を作成する。%in% は二つのベクトル間の要素の一致を確認するための演算子で、下記mutateコマンドでは、ind_en 列に書かれている情報が retail リストに「含まれる」か否かをチェックしている。そのため、以下コマンドでは、事前に作成した retail を参照し、ind_en で観察されるカテゴリーが retail に当てはまれば、"Retail"を、そうでなければ、"Others" を返すように指示していることになる。
library(tidyverse)
#産業名を特定したオブジェクト"Retail"の作成
retail <- c("Retail Stores, NEC", "Supermarket Chains")
# Retailを使ったカテゴリー変数の作成
firmdata19 <- firmdata19 %>%
mutate(format = ifelse(ind_en %in% retail, "Retail", "Other"))
#カテゴリーの頻度チェック
with(firmdata19, table(format))## format
## Other Retail
## 98 49そして、作成したカテゴリー変数も含めて、以下のような回帰モデルを分析する。
##
## Call:
## lm(formula = op ~ mkexp + format, data = firmdata19)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.09224 -0.03182 -0.00752 0.01799 0.26461
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.098489 0.008859 11.117 < 2e-16 ***
## mkexp -0.069204 0.025444 -2.720 0.00734 **
## formatRetail -0.023734 0.009751 -2.434 0.01616 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05454 on 144 degrees of freedom
## Multiple R-squared: 0.1042, Adjusted R-squared: 0.09178
## F-statistic: 8.377 on 2 and 144 DF, p-value: 0.0003617上記のように、カテゴリー変数(format)を回帰モデルに含めるだけで、自動的にダミー変数化して分析を実行してくれる。今回はたまたま我々の意図通り Othersをベースライングループに設定されているが、これは、指示した結果ではない。 もし確実に特定のカテゴリーを1と定義したい場合には、自身でダミー変数を作成して回帰分析を行えばいい。
firmdata19 <- firmdata19 %>%
mutate(retail = ifelse(format == "Retail", 1, 0))
#確認
with(firmdata19, table(retail, format))## format
## retail Other Retail
## 0 98 0
## 1 0 49##
## Call:
## lm(formula = op ~ mkexp + retail, data = firmdata19)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.09224 -0.03182 -0.00752 0.01799 0.26461
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.098489 0.008859 11.117 < 2e-16 ***
## mkexp -0.069204 0.025444 -2.720 0.00734 **
## retail -0.023734 0.009751 -2.434 0.01616 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.05454 on 144 degrees of freedom
## Multiple R-squared: 0.1042, Adjusted R-squared: 0.09178
## F-statistic: 8.377 on 2 and 144 DF, p-value: 0.0003617分析の結果、マーケティング支出と小売ダミーのどちらも営業利益率に対して負に有意な影響を持つことがわかった。したがって、小売企業はデータセット内の他の産業よりも利益率が低いといえる。