10.3 セグメンテーションの実行とクラスター分析

セグメンテーションでは、基準となる情報を選定し、その情報を用いて消費者の類型を発見する。その発見の方法として照井・佐藤（2023）では、（1）経験、（2）クラスタリング、（3）潜在クラス、の3つの方法を紹介している。経験によるセグメンテーションでは、マーケティング担当者の経験や既存のリサーチによる知見を参考に消費者を類型する。この方法は、十分な知識や経験が蓄積されており、基準となる情報が限定的かつニーズと関連的である場合には有効になる。例えば、消費者の年齢がニーズと関連していることがわかっている場合、年齢に基づくセグメンテーションは特別な分析を介さずとも有効な手法となりうる。しかしながら、経験的な知見が不足している場合には、セグメンテーションの信頼性を損なうことに加えて、考慮すべき情報が複数ある場合には、情報処理が複雑になり、類型化が困難になる。

クラスタリングによるセグメンテーションは、クラスター分析を用いたセグメンテーションである。基準となる情報を（多くの場合複数）選択し、その情報をもとに各観測の類似性を求めることで、類型化を行う。この方法は、多くの情報をセグメンテーションの基準として用いることができる点や、分析方法についての資料やソフトウェアが充実しているため、分析の実現可能性が高いという利点を持つ。本資料ではこのクラスター分析を中心に議論を進める。第三の潜在クラスによるセグメンテーションでは、潜在クラスモデルと呼ばれる統計モデルを用いた方法である。これは発展的な手法であり、セグメントに関する統計的推測も行えるという利点を持っている。また、この方法では消費者が確率的に複数のグループに属することも許容するため、より現実的な手法とも評価されている（照井・佐藤,2023）。しかしながら、この方法には相対的に多くのデータを必要とし、発展的な統計的知識が必要になる。本講義においては潜在クラスモデルを用いた手法は扱わない。

本資料では、消費者や顧客のセグメントを発見するための方法としてクラスター分析を紹介する。クラスター分析は、2つ以上の基準となる情報（変数）に基づいて、対象または人を相互に排他的で網羅的なグループに分類するために使用される統計的手法である。クラスター分析にはいくつかのアプローチが存在するが、それらに共通するのはサンプル間の類似性を確認し、グループとして分割していくというプロセスを有しているということである。ここでは主に階層的クラスター分析と、被階層的クラスター分析を紹介する。階層的クラスター分析は類似する観測同士を段階的にまとめていき、グループ（クラスター）を形成していく方法である。一方で非階層的クラスター分析は、分析者の定めた前提のもと、非階層的にクラスターを形成する方法である。本資料ではおもに、これら2つのアプローチについて紹介する。

10.3.1 階層的クラスター分析

本節では、階層的クラスター分析について説明する。階層的クラスター分析では、データの中から類似している観測値を段階的にクラスターとしてまとめていき、最終的にすべてのデータが1つのクラスターになるまでそれを繰り返す方法である。

このプロセスにおいて類似度は観測値同士の距離として測られる。距離の測定方法には色々とあるが、ここではユークリッド距離とマンハッタン距離を紹介する。ユークリッド距離は、観測値同士の各座標の差の二乗和の平方根であり、マンハッタン距離は観測値同士の各座標の差の絶対値の合計であるといえる。例えば、以下の図10.2 における2点をつなぐ赤い線がユークリッド距離、青い線がマンハッタン距離だといえる。以降では、実際の分析においても頻繁に用いられるユークリッド距離に主に焦点を合わせ、手法を紹介する。

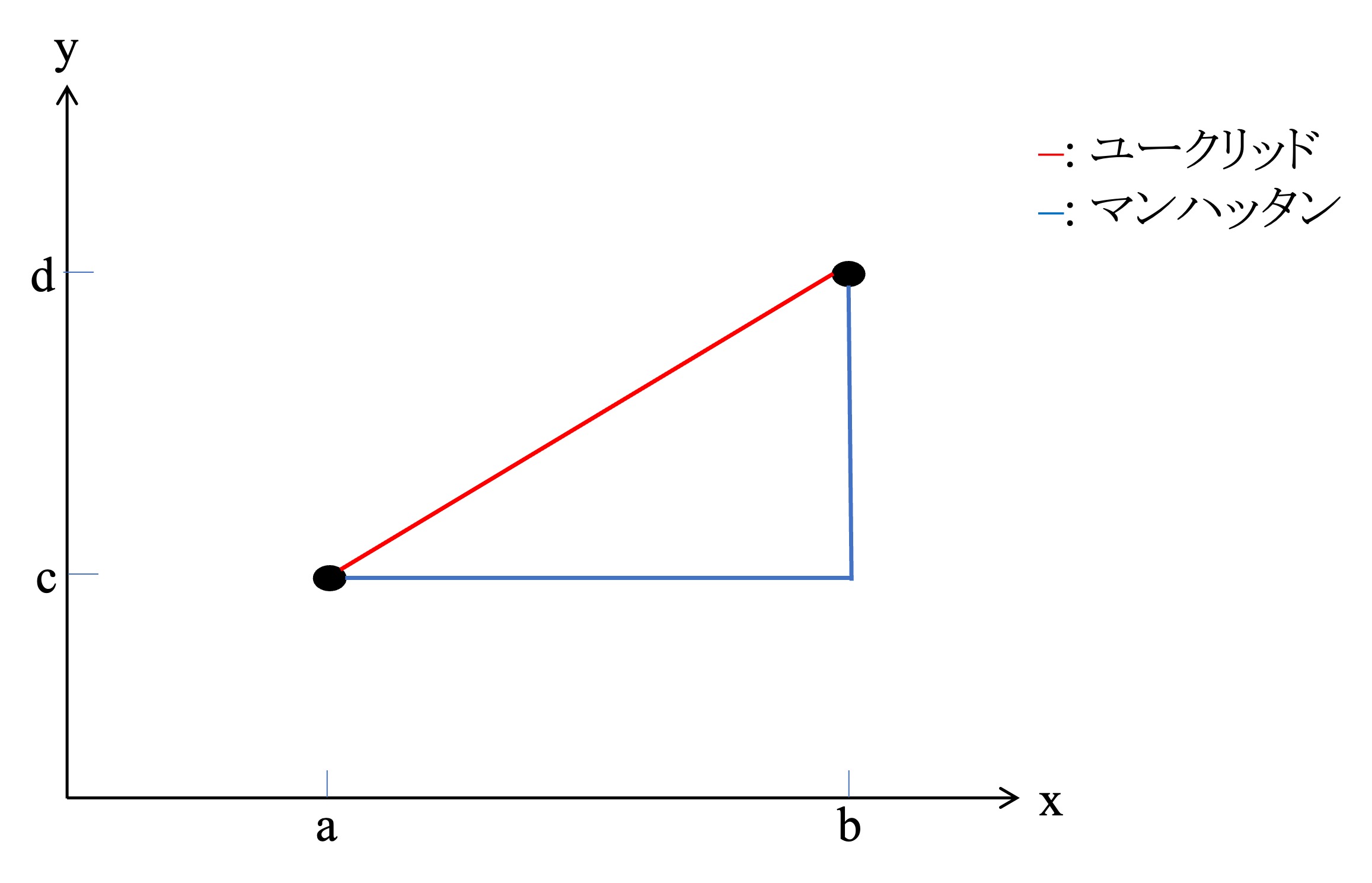
Figure 10.2: 距離定義概要

階層的クラスター分析では、図10.4 で示されているデンドログラム（樹形図）を得ることで、各観測が段階的に集約されていく様子が可視化される。例えば、図 10.4の左（1）では、6個の観測が3つのクラスターにまとめ・分類されている一方で、右（2）では、2つのクラスターに集約されている事がわかる。これらの図を見ると、aはbと最も近く、cはdと最も近いことがうかがえる。また、aとbで構成されたクラスターは、cdクラスターとは近いが、efとは遠いことがうかがえる。デンドログラムの解釈方法については後述するが、まずはデンドログラムを得るプロセスについて説明する。

ここでは、以下の表10.1 で示されている、2つの変数（x, y）に関する6個のデータが与えられた場合を考える。この場合の各観測値は図 10.3のように示される。

Table 10.1: データ例
	x	y
a	1	2
b	2	3
c	2	5
d	3	5
e	7	2
f	6	3

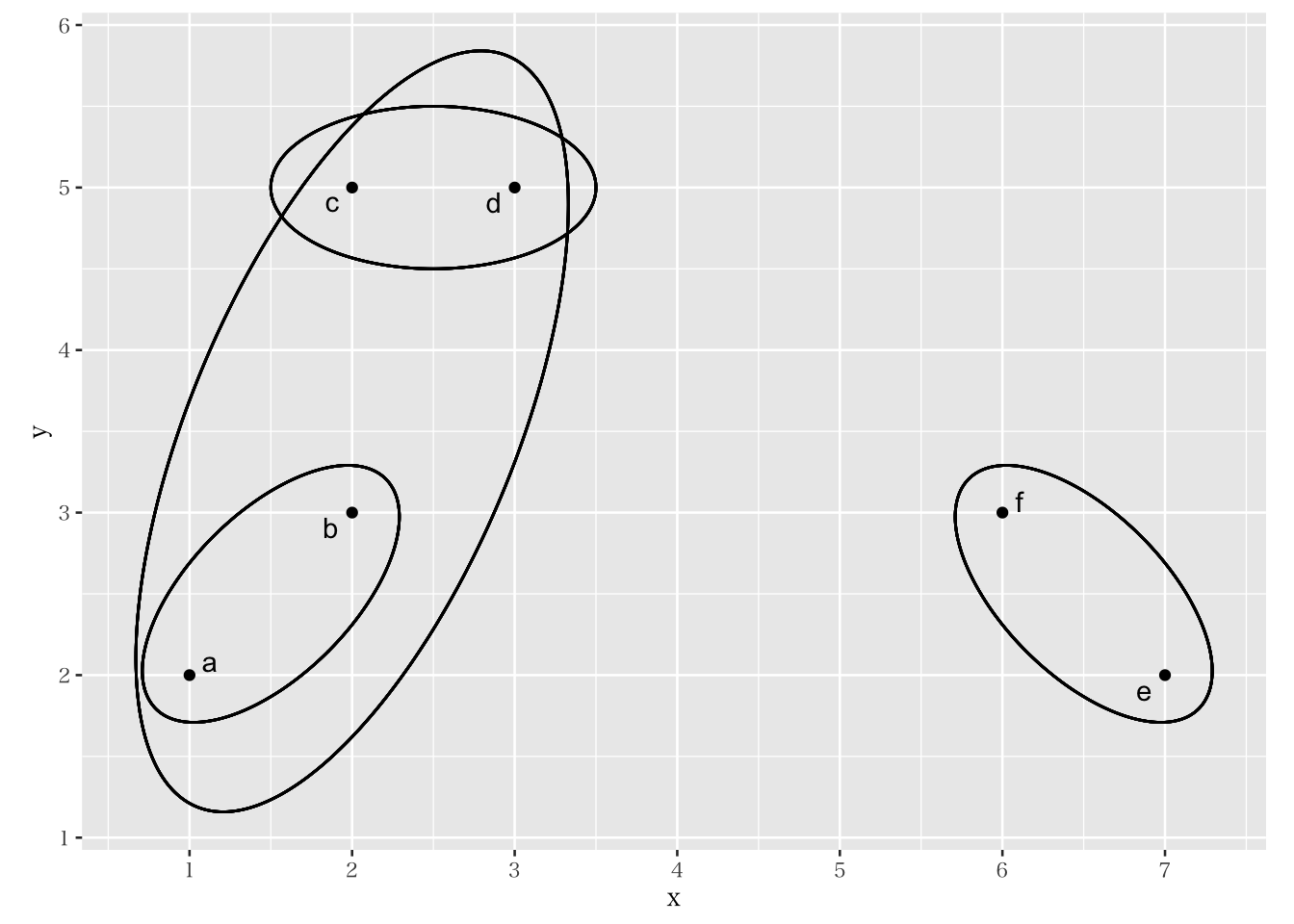
Figure 10.3: 階層的クラスター分析

この時、各データ同士の類似度をユークリッド距離で測るとする。例えば、a と最も近いデータは b である。a と b の距離は、以下のように求まる。 \[ \sqrt{(2-3)^2+(1-2)^2}=\sqrt{2}=1.414 \] 同様に、c（e）と最も近いデータは d（f）であり、その類似度もユークリッド距離で求めることができる。これによって、各観測点から最も近い観測点同士を結びつける形で、3つのクラスター（図10.4 左に対応）が初期段階のものとして形成される。次に、まとめた3つのクラスターと、他の観測点もしくは他クラスターとの距離を計算し、より大きな（多くの観測点が含まれる）クラスターを形成する。例えば、クラスター（a, b）は、（e, f）よりも（c, d）のほうに近いため、図10.3 に示されているように、（a, b, c, d）というクラスターとしてまとめる（合併する）ことができる（図10.4 右に対応）。このように段階的にデータをまとめていくと、最終的にはすべてのデータを一つのクラスターとしてまとめることができる。これが、階層的クラスター分析の直感的プロセスである。

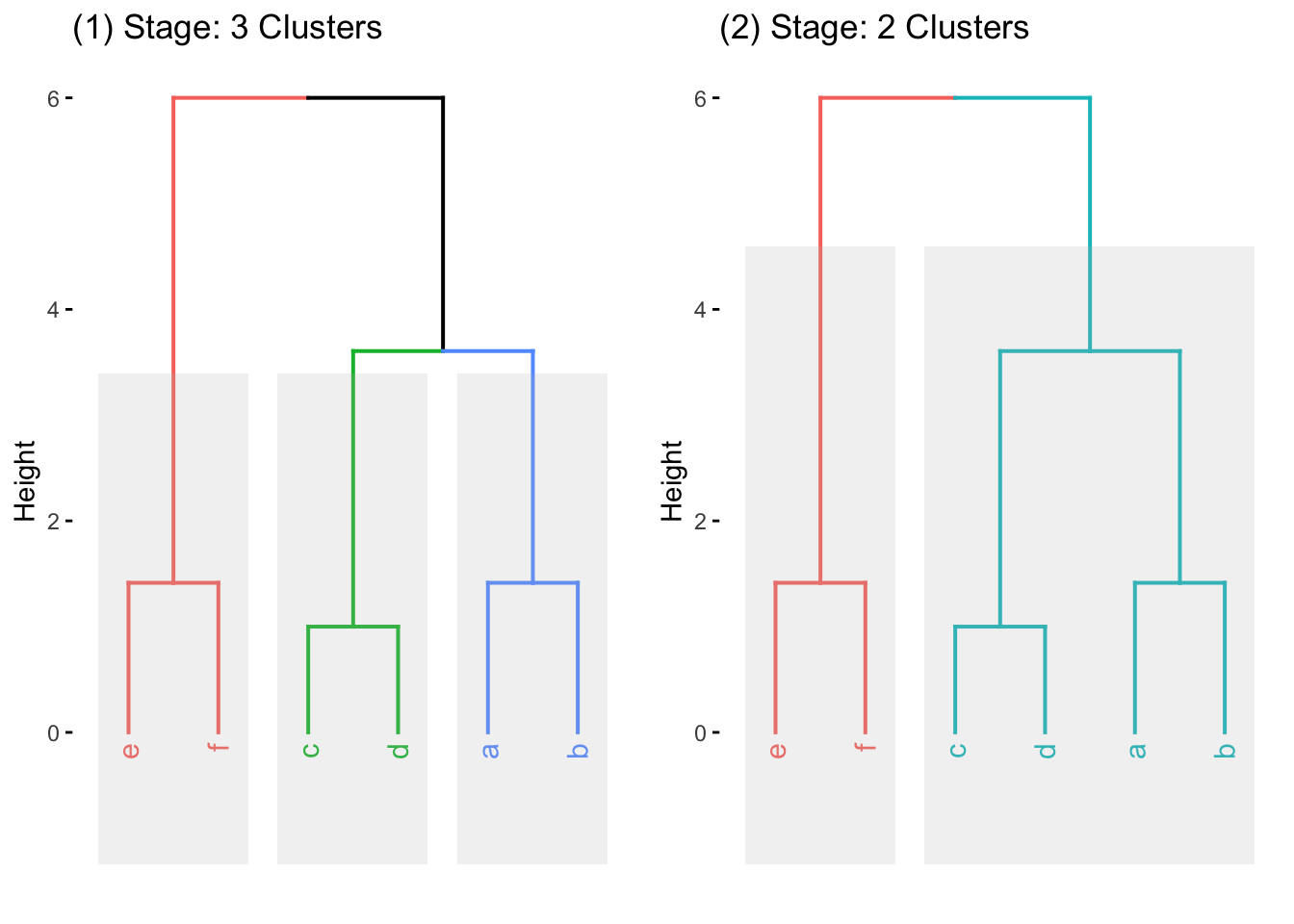
Figure 10.4: デンドログラム

図 10.4 のようなデンドログラムでは、一番下に全観測値が表示される。横軸と平行の線は、クラスタとしての併合を意味しており、下でのつながりほど初期に併合されたクラスタであることを示す。そのため、最終的には（一番上では）すべてが一つのクラスタにまとまっていることがうかがえる。この時、デンドログラムの高さ（縦軸）は距離を示している。したがってデンドログラムは、どの程度の離れ具合を許容するかによって何組でデータをまとめられるかが変わることを表している。例えば図10.4 では、高さを2に定めれば3つのクラスターにまとめることができ、4を設定すれば2つのクラスターにまとめることができる。

階層的クラスター分析ではクラスター同士を段階的に合併させていくのだが、クラスター同士の類似性を測るための方法もいくつか存在する。ここでは、代表的なものをいくつか紹介する。クラスター同士の距離の決め方として、図 10.5 に示すように、最短距離法（Single linkage method）、再遠距離法（Complete linkage method）群平均法（Group average method）がある。最短（遠）距離法はクラスタ間の最も近い（遠い）観測の組み合わせの距離を測るものである。一方で群平均法は、クラスタ間のすべての観察の組についての距離を計算する方法である。

また、非常に頻繁に使われる手法としてウォード法も存在する。ウォード法は最小分散法とも呼ばれ、クラスター内の平均までの二乗距離を最小化する方法である。

Figure 10.5: クラスター類似性測定手法

ウォード方では、異なるクラスター間の類似性について、まずそれらを構成する観測値を一括にして捉えた仮のクラスターを形成し、そのまとめられたクラスター内の観測値同士の距離が近い（分散が小さい）ものから併合される。図 10.6ではその直感的な概略図を示している。ウォード法ではこのようにクラスター間の類似性を分散の形式で測定することで段階的に併合するグループを決定していく。

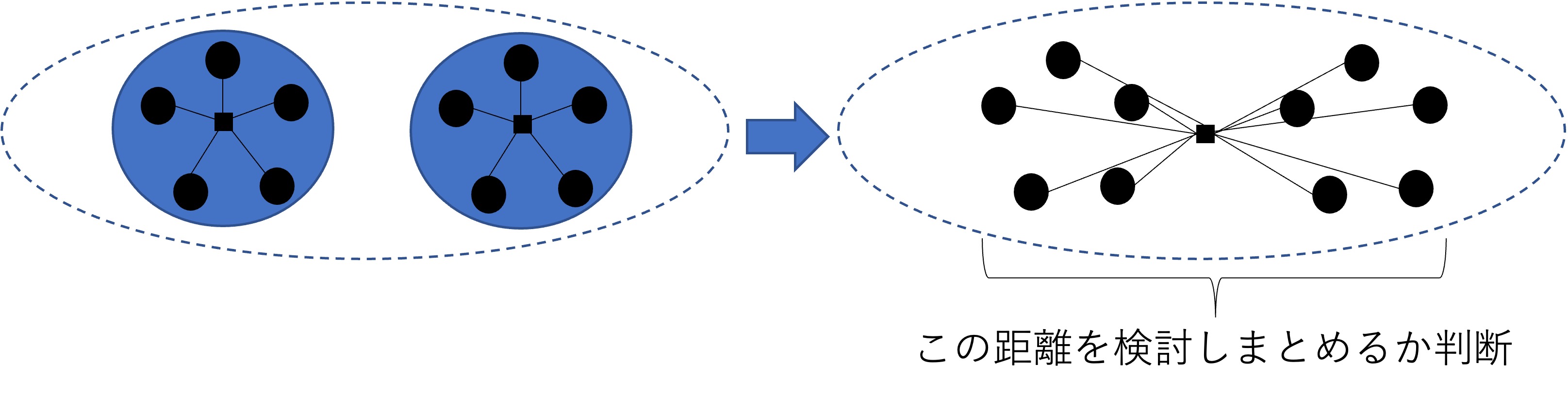
Figure 10.6: クラスター類似性測定手法

階層的クラスター分析におけるクラスター数の決定は、分析者の判断に依存し、絶対的な基準は存在しない。しかしながら、多くの場合、分類の「効率性」と「有効性」のバランスから効果的なクラスター数が決定される。効率性は分類によってどれだけ多くの情報を説明できているかを表しており、より少ないクラスター数で多くのデータを説明できたほうが情報の集約による効果が大きいと考えられる。例えば、表 10.1 で示されているような6つのデータを6つのクラスターで説明しても、クラスター分析としては不適切だといえる。一方で、得たクラスター分類がどの程度現実的に含意のある分類をできているか、を捉えたのが有効性である。効率性を意識しすぎて少ないクラスター数による分類を採用しても、あまりに大雑把過ぎる分類だと分析結果が有益にならない。例えば、図 10.3 において、1つのクラスターで6個のデータを説明するよりも、2つか3つのクラスターで説明したほうがより直感的かつ実務的な含意を得ることができるかもしれない。このように、階層的クラスター分析は、クラスターがどのように形成されていくかの段階を示すことによって、おおよそどのようなクラスター分類を行うことが良さそうかを判断することにつながる。