7.1 確率モデル、期待値と分散
伝統的なデータ分析では、標本から得た情報に基づき母集団の性質について推測する。母集団とは確率分布であり、標本はその確率分布に従う確率変数、データはその確率変数の実現値だと解釈できる(倉田・星野、2011)。そのうえで確率とは、起こりうる事象の集合内において、各事象の起こりやすさの度合いを0以上1以下の実数で表したものである。より詳細な定義として、標本空間を \(\small \Omega\)、任意の事象 A に対して実数 P(A) が定まっていて、以下の三つを満たすとき、P(A)は事象 A の確率という:
- 確率は非負であり、以下を満たす: \[0\leq P(A)\leq 1\]
- 全事象を \(\Omega\)、空事象を \(\emptyset\) とするとこれらの確率は以下の様に示される: \[P(\Omega)=1,~~ P(\emptyset)=0\]
- 事象 \(A_1,A_2,...\) が互いに排反ならば、これらのうち少なくとも1つが起こる事象 \(A_1\cup A_2\cup ...\) の確率は以下となる:
\[ P(A_1\cup A_2\cup ...)=P(A_1)+P(A_2)+... \]
確率変数とは、ある標本空間上で定義される取りうる各事象に対してそれぞれ一定の確率と対応関係のあるような変数である。例えば、細工のないサイコロを投げるとき、出た目の値を \(x\) とすると、\(x\) は1から6までの整数を取りうる変数だと言い換えることができる。この場合標本空間は、取りうる出目に対応した6個の標本点からなる。またこれらの標本点には、それぞれ対応する確率が以下のように付与されている。
| x | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 確率 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
このように、確率変数の取る値に対応して確率が付与されるルール( \(x\) の関数としての確率 \(P(x)\) )を確率分布や確率分布関数という。確率変数は主に、離散確率変数と連続確率変数に分けることができる。離散確率変数は、サイコロのように、取りうる値が離散的な確率変数である。一方で、連続確率変数は、ある範囲の中で連続的にどんな値も取りうる確率変数である。離散確率変数では、サイコロの表で示されているように、取りうる特定の値に対応する確率を確率分布に基づき計算できる。
一方で連続確率変数の場合、取りうる値の数が無限に存在する。例えば、-1 から 1 までの区間を取りうる値の範囲とする連続確率変数があったとする。この変数は例えば、0.90という値を取りうるが、同様に、0.91 や 0.900001 といった値も取りうる。このように、連続確率変数が取りうる値の数は無限に存在するため、取りうる特定の値に対応する確率は0になる。もし取りうる各値に確率が付与されていると、確率の合計が無限大になってしまうという問題に直面する。そのため、連続確率変数の場合、取りうる区間に対して確率が付与される。これを踏まえて連続確率変数を捉え直すと、連続確率変数は、その取りうる任意の区間に対して一定の確率が対応するような変数であるといえる。また、連続確率変数における取りうる区間の起こりやすさには「確率密度」が対応することで計算可能になる。言い換えると、確率変数 \(x\) の値に確率密度がどのように対応するのかという関係は、\(f(x)\) という確率密度関数(probability density function: PDF)として示される。PDF \(f(x)\) を持つ連続確率変数 \(x\) が区間 [a, b] を取る確率 \(P(a\leq x \leq b)\) は、以下の積分計算で求められる。
\[ P(a\leq x \leq b)=\int^b_a f(x) dx \]
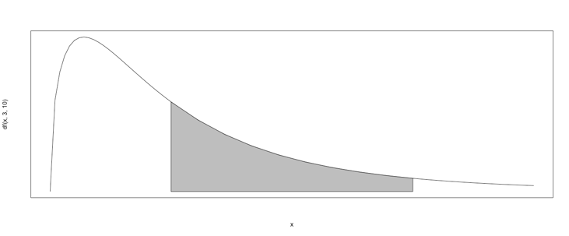
以下の図はPDFの例であり、図内の曲線はPDFを、灰色に塗られている面積はある区間の確率を示している。なお、上記の式で示されている関係から、PDFを特定(仮定)することで、ある確率に対応する区間 [a, b] を求めることも可能である。以降の節で紹介する統計的分析では、この関係を用いて分析することもあるが、詳しくは後述する。
連続確率変数を用いた具体的な確率計算例を紹介するために、ここでは一様分布(uniform distribution)を用いる。区間 [a, b] を持つ一様分布に従う確率変数 \(x\) のPDFは以下のように示される。
\[
f(x) =
\begin{cases}
\frac{1}{b-a} & a\leq x \leq b\\
0 & otherwise
\end{cases}
\]

具体的な計算を実行するために、ここで区間 [-1, 3] を持つ一様分布を考える。この一様分布のPDFは、\(\small f(x)=\frac{1}{4}~for~-1\leq x\leq 3\)(その他の区間の確率は0)となる。このとき、\(x\) が区間 [0, 2] を取る確率は、以下のように求められる。
\[ P(0\leq x \leq 2) = \int^2_0 \frac{1}{4} dx=\left[\frac{x}{4}\right]^2_0=\frac{1}{2}-0=\frac{1}{2} \] 次に、期待値を求める。期待値とは確率の考え方を含む理論的な平均値(\(\mu\))といえる。確率分布 \(P(x)\) を持つ離散確率変数 \(x\) の期待値 \(E(x)\) は一般的に以下のように定義することができる:
\[ E(x) = \sum_x x \cdot P(x)=\mu \] 一方、PDF \(f(x)\) を持つ連続確率変数 \(x\) の期待値 \(E(x)\) は一般的に以下のように定義することができる:
\[ E(x) = \int_{-\infty}^\infty x \cdot f(x) dx=\mu \] この定義に基づき、先程の区間 [-1, 3] を持つ一様分布の期待値を以下のように求める。
\[ E(x)= \int^3_{-1} \frac{x}{4} dx=\left[\frac{x^2}{8}\right]_{-1}^3=\frac{9-1}{8}=1 \]
期待値 \(E(x)\) は一般的に、\(a\) を定数、\(g(x)\) と \(h(x)\) を \(x\) の関数とするとき、以下が成り立つ:
- \(E(a) = a\)
- \(E[a\cdot g(x)]=a\cdot E[g(x)]\)
- \(E[g(x)+h(x)]=E[g(x)]+E[h(x)]\)
これらの性質により、確率変数 \(x\) の分散(\(\sigma^2\))は以下のように求まる。つまり、分散は二乗の期待値から期待値の二乗を引くことで計算できる。
\[ \sigma^2=E\left[\bigl(x-E(x)\bigr)^2\right]=E\left[(x-\mu)^2\right]=E(x^2)-E(x)^2 \]