8.4 重回帰モデル2
8.4.1 回帰係数の解釈
ここからは、重回帰分析の係数の解釈について説明する。ここで説明する解釈は、なぜ基本的には重回帰モデルを採用すべきなのか、を理解するために重要な内容である。結論から述べると、重回帰分析における説明変数の係数は、同モデル内の「他の変数の効果をコントロールしたうえで」説明変数が被説明変数へ与える影響を表している。そして重回帰分析のこの特徴が、学術的にも実務的にも重要な含意を与えうる分析手法として機能する。
重回帰モデルにおける各説明変数の係数は、パーシャル効果として解釈できる。以下では、このパーシャル効果の直感について、Wooldridge(2013)を参考に説明する。まず、以下のような説明変数が二個である重回帰モデルを考える。
\[ y_i=\beta_0+\beta_1x_{1i}+\beta_2x_{2i}+u \] そして、上モデルの予測値は以下のように示すことができる。
\[ \hat{y}_i=\hat{\beta}_0+\hat{\beta}_1x_{1i}+\hat{\beta}_2x_{2i} \]
このとき、説明変数 \(\small x_1\) と \(\small x_2\) の変化を \(\small \Delta x_{1i}\) と \(\small \Delta x_{2i}\) とすると、予測値の変化(\(\small \Delta \hat{y}\))は以下のように表すことができる。
\[ \Delta\hat{y}_i=\hat{\beta}_1\Delta x_{1i}+\hat{\beta}_2\Delta x_{2i} \]
ここで、\(\small x_2\) を固定(\(\small \Delta x_{2i}=0\))すると、以下を得る。
\[ \Delta\hat{y}_i=\hat{\beta}_1\Delta x_{1i} \] つまり、重回帰モデルにおける \(\hat{\beta}_1\) は、別の説明変数をコントロール(\(\small \Delta x_{2i}=0\))した上で、\(\small x_1\) が \(\small \hat{y}\) に与える影響(\(\small x_1\) が変化した際の \(\small \hat{y}\)の変化の程度)を捉えていると解釈できる。また、\(\small \hat{\beta}_2\) についても同様に解釈できる。そしてこの特徴は、k個の説明変数を用いたモデルにも同様に適応できる。なお、パーシャル効果に関するもう少し詳細な説明は本書では割愛する。
では、このパーシャル効果という重回帰モデルの特徴は、どのように応用できるのだろうか。多くの実証研究では、重回帰モデルの特徴を利用し、「コントロール変数」を用いた分析を行っている。本節では、先程の企業データを用いて、「企業の広告支出が営業利益に与える影響を明らかにする」という問いを考える。まずは、学習的意図から以下のように単回帰分析を実施してみる(通常の論文・レポートであればこのようなプロセスを記載する必要はない)。
##
## Call:
## lm(formula = operating_profit ~ adv, data = firmdata19)
##
## Residuals:
## Min 1Q Median 3Q Max
## -450515 -55314 -40160 -1096 599313
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.685e+04 1.050e+04 5.414 2.49e-07 ***
## adv 1.258e+00 2.152e-01 5.846 3.20e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 117200 on 145 degrees of freedom
## Multiple R-squared: 0.1907, Adjusted R-squared: 0.1852
## F-statistic: 34.18 on 1 and 145 DF, p-value: 3.197e-08## 2.5 % 97.5 %
## (Intercept) 3.609692e+04 77602.573216
## adv 8.325719e-01 1.683065分析の結果、広告支出(adv)の係数は正に有意であり、その95%信頼区間は [0.83, 1.68] であることが確認できた(8.325719e-01は0.8325719)。
しかしながら、このモデル化は不十分であり他の要素も考慮すべきである。営業利益に影響を与えうる要因は色々とあり 、実際の研究においては先行研究を参照しつつ、コントロールすべき変数を含める形で回帰モデルを特定する必要がある。しかしながら、ここでは便宜上いくつかの要因にのみ焦点を合わせて簡単に特定化する。本データは主に小売・サービス産業の企業に焦点を合わせている。そのため、対人サービス水準は企業のパフォーマンスに影響を与えうる要因である。そのため、従業員に関する変数(従業員数: emp、パートタイム従業員数: temp)と人件費(labor_cost)をモデルに含める。また、資産合計(total_assets)、研究開発費(rd)もモデルに含める。今回の回帰モデルは以下のように示される。
\[
\text{opretating_profit}_i = \beta_0 + \beta_1 adv_i + \beta_2emp_i+\beta_3temp_i+\beta_4\text{labor_cost}_i+\beta_5\text{total_assets}_i+\beta_6rd_i+u_i
\]
Rにおいて重回帰分析を実行するのは簡単である。lm(y ~ x1 + x2 + x3) のように \(+\) 記号と変数を追加すれば、重回帰モデルとして分析を実行してくれる。
reg3 <- lm(operating_profit ~ adv + temp + emp + labor_cost + total_assets + rd, data = firmdata19)
summary(reg3)##
## Call:
## lm(formula = operating_profit ~ adv + temp + emp + labor_cost +
## total_assets + rd, data = firmdata19)
##
## Residuals:
## Min 1Q Median 3Q Max
## -360570 -27367 -14970 3349 284990
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.168e+04 8.056e+03 2.691 0.00800 **
## adv -1.430e+00 2.946e-01 -4.852 3.22e-06 ***
## temp -1.866e+00 6.292e-01 -2.965 0.00356 **
## emp -1.489e+00 7.008e-01 -2.125 0.03533 *
## labor_cost 8.770e-01 1.686e-01 5.202 6.86e-07 ***
## total_assets 3.507e-02 5.823e-03 6.023 1.43e-08 ***
## rd 1.380e+00 5.254e-01 2.627 0.00957 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 78740 on 140 degrees of freedom
## Multiple R-squared: 0.6474, Adjusted R-squared: 0.6323
## F-statistic: 42.84 on 6 and 140 DF, p-value: < 2.2e-16## 2.5 % 97.5 %
## (Intercept) 5749.50978947 3.760568e+04
## adv -2.01201729 -8.470087e-01
## temp -3.10966464 -6.216177e-01
## emp -2.87467416 -1.038058e-01
## labor_cost 0.54369783 1.210293e+00
## total_assets 0.02355591 4.657974e-02
## rd 0.34159701 2.419018e+00見ての通り、結果の出力方式も単回帰分析のものとほぼ同様である。回帰係数の結果下にあるモデル適合度については前のサブセクションを参照して欲しい。
分析の結果、広告支出の係数は「負」に有意であり、その信頼区間も [-2.01, -0.84] であった。したがって、本データの分析によると、労働や資産に加え研究開発といった側面を一定とすると、広告支出は営業利益に負の影響を与えることがわかった。他の変数に着目すると、従業員数に関する変数はどちらも負に有意であった。一方で、人件費と総資産、研究開発費は正に有意な影響を与えることが示された。これらの結果から、単純に従業員数を増やしても営業利益には負の影響を与える一方で、従業員数を一定とした上で人件費を上げるほうが営業利益が高いことが示された。また、資産や研究開発費も営業利益につながることが示された。
このように、重回帰モデルを採用し複数の説明変数を含めることで、各係数の持つ含意が大きく変わることに注意して欲しい。また、reg2 と reg3の比較のように、特定の説明変数に対応する係数の符号が変わることも珍しくない。そのため、回帰モデルの定式化には非常に慎重になる必要があり、先述の通り、先行研究を参照して必要な変数をコントロールすることが求められる。
また、これらの結果を踏まえて、3.1節で強調した「マネジメントとリサーチの分離」の重要性を思い出して欲しい。あなたが reg2 と reg3の分析を実施したリサーチャーであり、本リサーチのクライアントがマーケティング・広告部門の部長だっとしよう。そして、(1)あなた自身もマーケティング部門の社員であり、クライアントは直属の上司、(2)あなた自身はクライアントとは無関係の立場、という二つの異なる立場に立っている状況を想像して欲しい。(1)の場合、逆恨みによるあなた自身への不利益を恐れて重回帰分析の結果を「ありのまま」伝えられないかもしれない。もちろん研究倫理に基づけば、都合の良い研究成果を作為的に発表することは問題であり、そのようなことはすべきではない。したがって研究成果を「ありのまま」を伝えるべきであり、都合のいい結果を発表する決断をした人(リサーチャー)が悪い。しかしながら、その背後にある利害関係を鑑みれば、reg2
の結果を報告したくなる人がいることも理解できる。個人の判断を批判するだけでなく、このような研究不正を働く誘因や構造についても考慮すべきである。例えば、上記のようなリサーチャーをとりまく利害関係には気をつけなければならない。なお、定量的な分析に慣れている研究者からすると、特別な理由がないにも関わらず重回帰でなく単回帰分析を用いるのは不自然な分析アプローチである。そのため、 もし調査・分析の設計上意図的に単回帰分析を実施する場合には、その意図と有用性をきちんと説明すると良い。
8.4.2 重回帰モデルにおける変数選択
重回帰モデルでは、複数の説明変数を採用することができるため、どの変数をモデルに含めるべきかという点を考察しモデルを特定化する必要がある。このような説明変数の選択に関わる問題として、本サブセクションでは、欠落変数バイアス、多重共線性、過剰統制の三つを紹介する。まず、欠落変数バイアスについてだが、本来含めるべき変数を含めずにモデルを定式化し推定を行うと、推定された係数にバイアスが生じ、OLSEが不偏推定量でなくなるという問題が生じる。また、このバイアスの方向(正負)は欠落された変数と被説明変数との真の関係(欠落された変数が被説明変数に対して持つ母集団での回帰係数)と、モデルに含まれる説明変数と欠落変数との相関で決まる(Wooldridge, 2013)。以下で欠落変数バイアスについての簡単な説明を提示する。
はじめに、以下の式が正しいモデルだと仮定する。 \[ y=\beta_0+\beta_1x_1+\beta_2x_2+u \] これに対して\(x_2\)を含まずに欠落変数モデルを推定した場合、以下のような結果を得る。
\[ \tilde{y}=\tilde{\beta}_0+\tilde{\beta}_1x_1 \] このとき、真のモデルの推定値(\(\small \hat{\beta}_1\))と \(\small \tilde{\beta}_1\) の間には、以下の関係がある。
\[ \tilde{\beta}_1=\hat{\beta}_1+\hat{\beta_2}\tilde{\delta_1} \] ただし、\(\small \tilde{x}_2=\tilde{\delta}_0+\tilde{\delta}_1x_1\)とする。つまり、\(\small \tilde{\delta}_1\) は \(\small x_1\) の \(\small x_2\) に対する回帰係数の推定値である。したがって以下のように、欠落変数モデルでは推定結果に\(\small \beta_2\tilde{\delta}_1\) の分だけバイアスが生じる。
\[ E(\tilde{\beta}_1|x_1,x_2)=E(\hat{\beta}_1)+E(\hat{\beta_2} \tilde{\delta_1})=\beta_1+\beta_2\tilde{\delta}_1 \] そして、欠落変数によってバイアスが生じるということが、重回帰分析の重要性を主張する根拠となる。そのため、仮に研究課題上ではあまり重要でない変数であっても、自身の関心のある説明変数の影響を分析するためにコントロール変数をモデルに含めることが重要になる。
第二の論点として、単回帰分析の際には存在しなかった多重共線性(multicollinearity)という問題がある。これは説明変数同士の相関が高いことによる推定上の問題であり、Variance Inflation Factor という指標9を使ってその程度を測ることもある。また、マーケティング領域の研究においてはまれに「多重共線性があるから、説明変数を除外すべきだ」という主張を聞くことがある。しかしながら、本書はできる限り説明変数の除外を行わないほうが良いという立場を提示する。詳しくは後述するが、分析の対象となる説明変数によって極端にVIFが高くなる場合には、次の段落にあるようにその変数の意義を検討し、その変数をそのまま残す、何かで比を取る、対数化する(詳しくは次章)などの変数変換の工夫をしながら、その変数をモデルに含めるということが現実的かつ実践的な対応となる。なおこの立場は、本書が回帰分析における係数の検証や解釈に注視していることに大きく依存するため、注意してほしい。
多重共線性について語る際には、(1) 説明変数同士が完全に相関している(相関係数が 1 もしくは -1)場合と、(2) 完璧ではないが相関係数が高い場合、という二つの異なる状況を区別し理解する必要がある。まず一つ目の場合、そもそも係数の推定値が計算できないという問題が生じる。そのため、完璧に相関しあっている変数を同時にモデルに含めることは出来ず、変数の除外を考えないといけない。この問題は言い換えると「同じ変数を同モデル内に複数入れてはいけない」という制約だと理解できる(西山ほか, 2019)。では(2)の場合にはどのような問題が生じるのか。結論から述べると、説明変数同士の相関は、推定量の分散 \(\small Var(\hat{\beta}_j)\) を高めてしまう(Wooldridge, 2013)。しかし、 \(\small Var(\hat{\beta}_j)\) は、多重共線性だけでなく以下の三つの要素から影響を受ける。第一に、誤差項の真の分散(\(\small \sigma^2\))、第二に独立変数間の相関10、第三に、独立変数の変動(\(\small SST_j=\sum(x_{ji}-\bar{x}_j)^2\))である。第一と第二の指標が高い場合には、推定量の分散は大きくなる。一方で、第三の要素である\(\small SST_j\) が高い場合には \(\small Var(\hat{\beta}_j)\) は小さくなる。そのため、\(\small Var(\hat{\beta}_j)\) を改善するためには、サンプルサイズを大きくし\(\small SST_j\) を大きくすることも有用な対処方法となる。しかしながら、社会科学分野においてはデータ取得可能性の観点からそれが難しいことも多い。そのときには、推定量分散の増加と説明変数除外による弊害とのトレードオフを考慮して意思決定することになる。そのうえで本書は、先述の通りできる限り説明変数を除外することは避けるほうが良いという立場を取る。必要な説明変数を含めずに回帰分析を行うと、欠落変数バイアスの問題が生じる。また、もし分析における主な関心が、着目する説明変数 \(\small x_{ji}\) の \(y_{i}\) への効果を検証・解釈することであり、かつそれをきちんと捉えるために他の説明変数の存在が必要なのであれば、VIFは無視して構わない(cf. Wooldridge, 2013)。そのため、「VIFが10以上11だから、多重共線性があり、変数を除外すべきだ」というような考えは、上記の研究上の関心に対しては恣意的であり有意義でないと考える。そもそも先述のように、VIFによって生じる問題は\(\small Var(\hat{\beta}_j)\) の増加であるが、この分散は他の要素にも影響を受けるため、VIFが10以上だから必ず \(\small Var(\hat{\beta}_j)\) が大きすぎて推定量が有用でないということはない。これらのことから、回帰モデルに含む変数選択は、VIFの値に依存して判断するよりも、分析モデルの意図や用いる変数の理論的・分析的意義について検討し決断されるべきものだと考える。
第三に過剰制御は、モデル内での係数解釈の変化を捉えた問題である。ここまでの説明では、欠落変数バイアスの議論を中心に、基本的には変数をモデルに含めることの重要性を説明してきた。しかしながら、重回帰分析の係数の解釈(パーシャル効果)を鑑みると、主要な説明変数の効果に関する理論的なメカニズムにおいて中間経路として機能する変数をモデルに含めることには注意が必要である。例えば、製品開発におけるクラウドソーシングという非専門家(一般消費者)の意見を製品開発に活用する戦略(e.g., Nishikawa et al., 2017)が製品の売上に与える影響を、製品レベルデータを用いて分析する場合を考える。その際、クラウドソーシングの有効性に関するメカニズムとして、実際の製品ユーザーである消費者の意見を反映することで、品質の高い製品を開発でき、結果として売上向上につながるというものを考えているとする。つまり、クラウドソーシングが売上に与える中間経路として、製品の品質が機能するというメカニズムを考えていることになる。しかしながら、売上を被説明変数とする回帰モデルを考える際に、製品品質も売上に影響を与えうる変数なので説明変数として回帰モデルに含めたいと考えるかもしれない。このような考えが、過剰制御の問題につながる。製品品質は、クラウドソーシングから売上への影響に関する中間経路として機能する変数であり、これをコントロールしてしまうことは、クラウドソーシングの係数の解釈を大きく変えてしまう。具体的には、このようなモデルでは、製品品質を一定とした上でクラウドソーシングが売上に与える影響を捉えることになってしまう。上記の関係は以下の図のように示される。
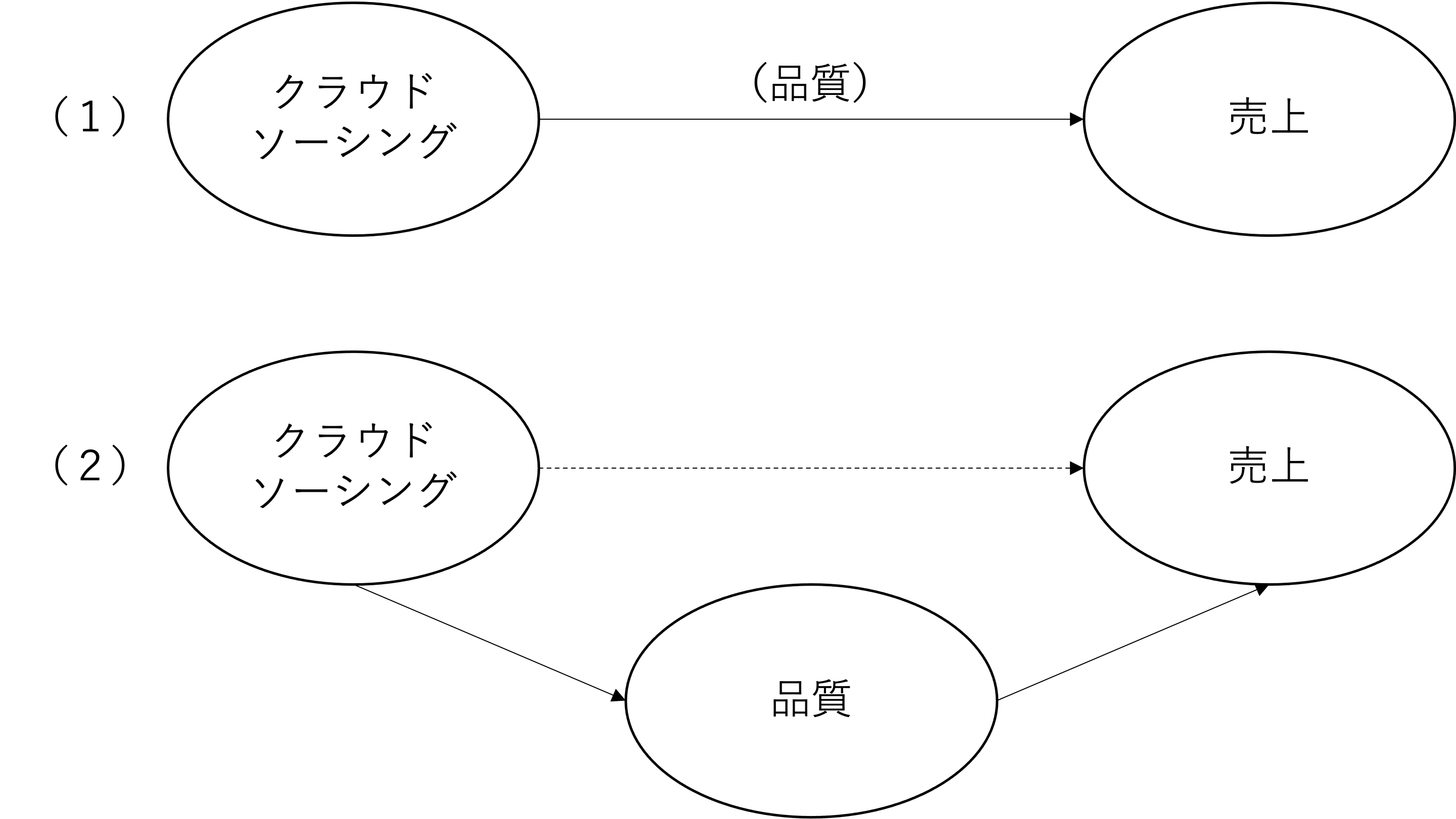
製品品質以外のクラウドソーシングの効果が研究の関心と整合的であるならば、品質を含めた定式化で問題はない。しかしながら、重回帰モデルの変数選択では、自身が論じているメカニズムと係数解釈の整合性を保つように、中間経路変数を含めることで過剰制御の問題に陥っていないかを慎重に検討する必要がある。
重回帰モデルに含める変数の指針について、西山ほか(2019, p.186)は以下の表のように整理している。なお、本書においては主に欠落変数バイアスと係数の解釈という観点から変数選択に関する考え方を整理した。これは、研究上関心のある変数の効果(係数)について検証・解釈するという観点に基づく議論である。しかしながら、「予測」という側面に着目すれば推定や予測の精度を高める(誤差を小さくする)ことが重要になり、変数選択の基準も変わる。そうなれば、欠落変数による問題や係数の解釈の変化はあまり重要でなくなるかもしれない。このように、立場が変わることによって回帰モデルの特定化の基準も変化することを最後に付け加えておく。
| x に影響を与える or x と同時決定 | x から影響を受ける | x とは無相関 | |
|---|---|---|---|
| y に影響を直接与える | 必ず含める(欠落変数を防ぐ) | 含めていけない(過剰制御) | 含めることで推定誤差は減る(含めなくてもバイアスは増えない) |
| y に影響を与えない | 含めないほうが良い(ただし推定誤差は増えるがバイアスは増えない) | 左と同様 | 左と同様 |