7.7 統計的仮説検定
データを用いた研究では、統計的分析によって提示した仮説が支持できるか否かを判断したいという目的を持つこともある。その時に用いられる方法が統計的仮説検定である。本節ではまず検定の手順について説明したあと、分析結果の意味や解釈について説明する。統計的仮説検定は、基本的に以下の手順によって実施される。
仮説(帰無仮説・対立仮説)を設ける。
仮説を検定するための統計量を選ぶ。
統計量の値について、有意確率に基づく臨界値を設定する。
帰無仮説が正しいと仮定した上で統計量を計算し、その値が棄却域と採択域のどちらの領域に入るかを分析する。
統計的仮説検定で重要になる仮説は、帰無仮説と対立仮説である。理解を容易にするために、「問題と分析をつなげる仮説の提示」という節で議論した仮説を「作業仮説」と呼ぶ。作業仮説は、リサーチクエスチョンに答えるための論理的予測である。例えば、「女性に比べ男性の方が新製品購買意図が高い。」のような予測が考える。このような仮説を検証する場合、男女(グループ)間で購買意図の平均値を比較することが現実的な分析方法として考えられる。
帰無仮説と対立仮説は、統計的仮説検定の基準になる母集団の統計的特徴に関する仮説であり、検定という手続き上ではこれらの仮説に着目する。特に、帰無仮説は、統計的仮説検定の考察、分析の基準となる仮説であり、この仮説を棄却(否定)できるか否かを調べることが基本的な統計的仮説検定の枠組みだと言える。帰無仮説は棄却しうる仮説であり、\(\small H_0\) という記号で表される事が多い。また、多くの場合において「差がない」、「効果がない(0である)」や、「特定の値と等しい」といった仮説が設計される。一方で対立仮説は、帰無仮説とは排反な仮説であり、帰無仮説が棄却された際に採用される推測であり、\(\small H_1\)や\(\small H_a\)という記号で表される。データ分析を用いた研究においては対立仮説と作業仮説は論理的に整合的ないしは等しいことが好ましい。つまり、作業仮説という研究上重要な論理的推測を検証するために、その作業仮説とは排反な帰無仮説を設計し統計的仮説検定を実施する必要がある。それによってもしその帰無仮説が棄却されたならば、対立仮説ひいては作業仮説がデータ分析によって支持されたと解釈することが可能になる。
先述の男女間の購買意図の差に関する作業仮説について、男性における購買意図の期待値を \(\small \mu_m\)、女性における購買意図の期待値を \(\small \mu_f\)とすると、帰無仮説と対立仮説は以下のように示すことができる。
- \(H_0:~\mu_m=\mu_f\)
- \(H_1:~\mu_m\neq\mu_f\)
\(\small H_0\) は、男性における購買意図の期待値と女性における期待値が等しいというものであり、 \(\small H_1\)はそれらが等しくないということを示している。そのため上記の二つの仮説は、どちらも未知パラメータについての関係を捉えており、\(\small H_0\) と \(\small H_1\) は互いに排反であることがわかる。その上で、もし帰無仮説が棄却され、男性の平均値のほうが女性よりも高い場合には、作業仮説が支持されたと解釈することができる。つまり統計的な検定においては、作業仮説として提示している推測を直接検証するのではなく、作業仮説と排反な帰無仮説を設計し、それが棄却されるならば暫定的に作業仮説の主張を指示しようという立場で検証を行う。なお対立仮説として\(\small H_1:~\mu_m>\mu_f\) を設定することも可能である。このような仮説に基づく検定方法は片側検定と呼ばれ、その詳細については後述する。
ここで改めて、より一般的な形でマーケティングリサーチで用いられる仮説と検定で用いられる仮説との関係を整理する。
- 分析上の基準である帰無仮説は何かをきちんと理解し定義する。
- それが棄却された際にはどのような結論(対立仮説)が採用されるのかを理解する。
- そしてその結論が自身の立てた作業仮説と帰無仮説・対立仮説の関係が整合的かを考える。
言い換えると、自身の立てた作業仮説を帰無仮説・対立仮説の対比という分析手続きで証明できるような調査・分析法を採用する必要がある。ただし、レポートや論文には、帰無仮説・対立仮説を記載せず、作業仮説のみを記載することがほとんどである。
先程の新型電球の例を再度使い母平均の検定を実施する。新型電球について我々が関心を持っていたのは、新型電球の製品寿命が旧型の寿命(1700時間)より長いか否かである。そのため、新型電球の製品寿命の期待値を \(\small \mu\) とすると、帰無仮説と対立仮説は以下のように設計できる。
- \(H_0:~\mu=1700\)
- \(H_1:~\mu\neq1700\)
改めて以下の通り、新型電球に関する16個の無作為標本から得た製品寿命の平均値を計算すると、\(\small \bar{X}=1835\) であった。では、この1835は 1700 から十分に離れていると言えるのだろうか?もし、十分に離れていると判断されれば帰無仮説を棄却するが、この差が十分でなければ帰無仮説を採択する。
## [1] 1834.688Rを用いて統計的検定を実行すること自体は難しくない。母平均の検定は t.test() で実施することが可能である。母平均が特定の値を取るか否かについての検定では、mu= という引数を使って帰無仮説に対応する値を指定する。今回の分析に関するコマンドおよびその結果は以下のとおりである。
##
## One Sample t-test
##
## data: bulb
## t = 2.6968, df = 15, p-value = 0.01657
## alternative hypothesis: true mean is not equal to 1700
## 95 percent confidence interval:
## 1728.235 1941.140
## sample estimates:
## mean of x
## 1834.688分析結果の t= と df = はそれぞれt値(検定統計量の推定値)と自由度を表している。p-valueはp値と呼ばれるある確率を表しており、この確率が小さい場合、帰無仮説を棄却する。また、t.test() は、信頼区間や標本平均も出力してくれるため、これらの結果に基づき解釈を行うことも可能である。帰無仮説の棄却に至るp値の基準は慣習的に、0.10(10%)、0.05(5%)、0.01(1%)が用いられる。今回の結果では、p値が0.016であり、5%水準で帰無仮説を棄却することができるため、新型電球の寿命は旧型(1700時間)よりも有意に高いと結論づけることができる。では、このp値とはどのような確率を示しているのだろうか?この点を理解するために統計的仮説検定についてもう少し深掘りしていく。
検定における統計量や有意確率について理解するために、再度新型電球の例を用いる。上述の t.test() は母分散が未知である際に用いられる検定方法である。この点は、信頼区間において説明した内容と同様である。なお実際のデータ分析作業においては多くの場合母分散は未知であるため、t.test() を用いることが多い。しかしながら、電球の例では母集団の分散は \(\small 180^2\) であることを仮定した。そのため、ここからは母分散が既知(\(\small \sigma^2=180^2\))であることを仮定した標準正規分布に基づく母平均の検定を軸に説明していく。
「区間推定」節の信頼区間の説明でも述べた通り、今回のように正規分布に従う母集団からの無作為標本 \(\small X_1,...,X_n\) の標本平均は以下の分布に従うことがわかっている8。
\[ \bar{X}\sim N\left(\mu,\frac{\sigma^2}{n}\right) \]
また、これまでの議論の通り、\(\small \bar{X}\)を標準化した統計量Zは以下の分布に従うことが知られている。
\[ Z=\frac{\bar{X}-\mu}{\sqrt{\sigma^2/n}}\sim N(0,1) \] ただし、今回の例においては、 \(\small \bar{X}=1835\)、\(\small= \sigma=180\) であることがわかっている。統計的仮説検定においては、この標準化された統計量を検定統計量(検定に用いる統計量)として用いて計算を行うのだが、我々の関心の中心でもある \(\small \mu\) は未知であり、通常この統計量を計算することはできない。すなわち、未知であるパラメーターを何かしらの値で代替しなければ、上記の検定統計量は計算できない。そこで、統計的な仮説検定では、「帰無仮説が正しいと一旦仮定」した上で統計量を計算するというプロセスを経る。言い換えると、未知のパラメーターについて帰無仮説で示されている値を代入することで、検定統計量を計算可能にする。
電球の例においては、\(H_0:~\mu=1700\)と設計していたため、検定統計量 Z は以下の通りに書き換えることができる。
\[ Z=\frac{1835-1700}{\sqrt{180^2/16}} \]
そして、もし「帰無仮説が正しければ」Zは標準正規分布に従うはずであり、言い換えると Z の計算結果は0に近い値を取る可能性が高いはずである。そこで、この Z を計算し、\(\small |Z|\) がある閾値 c よりも大きい(十分に0から離れている)場合には帰無仮説を棄却する。なお、ここで用いる閾値 c のことを一般的に臨界値と呼ぶ。つまり、検定統計量 Z の計算結果に対して、以下の方針で仮説検定を行うといえる。
\[ \begin{cases} |Z|>c & \Rightarrow \text{H0を棄却する。}\\ |Z|\leq c & \Rightarrow \text{H0を採択する。} \end{cases} \]
臨界値 c の求め方は区間推定と同様、分析に対応する確率分布(今回であれば標準正規分布)に基づくある区間の確率計算で求まる。研究者はまず、任意の確率 \(\small \alpha\) を決める。この確率は「有意水準(significance level)」と呼ばれ、この有意水準と標準正規分布に基づく確率計算によって臨界値(下図内では \(\small \pm z_{\alpha/2}\))を求める。その上で、統計量の計算結果が臨界値より外側(下図における斜線部)にある場合には帰無仮説を棄却する。そのため、斜線部のような領域を棄却域、確率 \(\small 1-\alpha\) に対応する範囲を採択域と一般に呼ぶ。
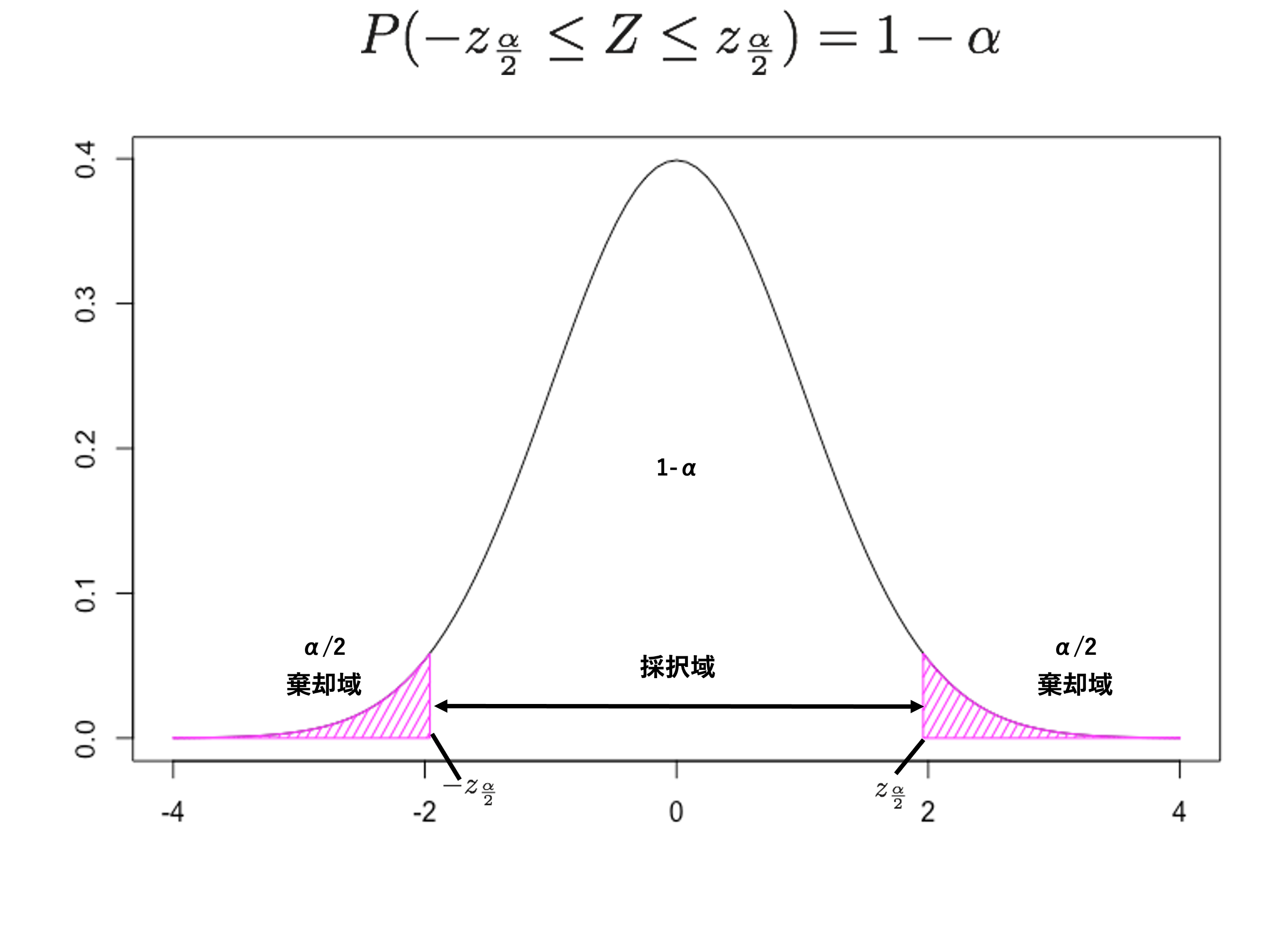
また、ここまでの例では対立仮説を \(H_1:~\mu\neq1700\) とし、左右対称の分布の両端に棄却域を設定した。このような検定方法を一般的に両側検定と呼ぶ。しかし、現実的ないしは理論的な根拠をもとに、ある値よりも高い(もしくは低い)ことが事前に予測できる場合がある。その場合には、例えば \(\small \mu>1700\) や \(\small \mu<1700\)といった対立仮説を設定することも可能である。このような対立仮説を利用した検定方法を一般的に片側検定と呼ぶ。ここでは、仮に\(\small \mu>1700\)という対立仮説を立てた場合を考えるが、\(\small \mu<1700\)のような対立仮説を設計しても正負を入れ替えることで同様の議論ができる。なお、片側検定において帰無仮説が棄却された場合、直ちに帰無仮説の値よりも大きい値を取ると判断する。しかしながら、たとえ異なる対立仮説を提示しても、採用する検定統計量や帰無仮説に基づく分布の仮定などは同じである。 片側検定を利用した場合の特殊性はその棄却域に現れる。片側検定の場合の棄却域は以下の図のように片側のみとなる。なお、その場合分布の両端に棄却域を設ける必要がないため、正の方向に \(\small \alpha\) 分の棄却域を設定する。
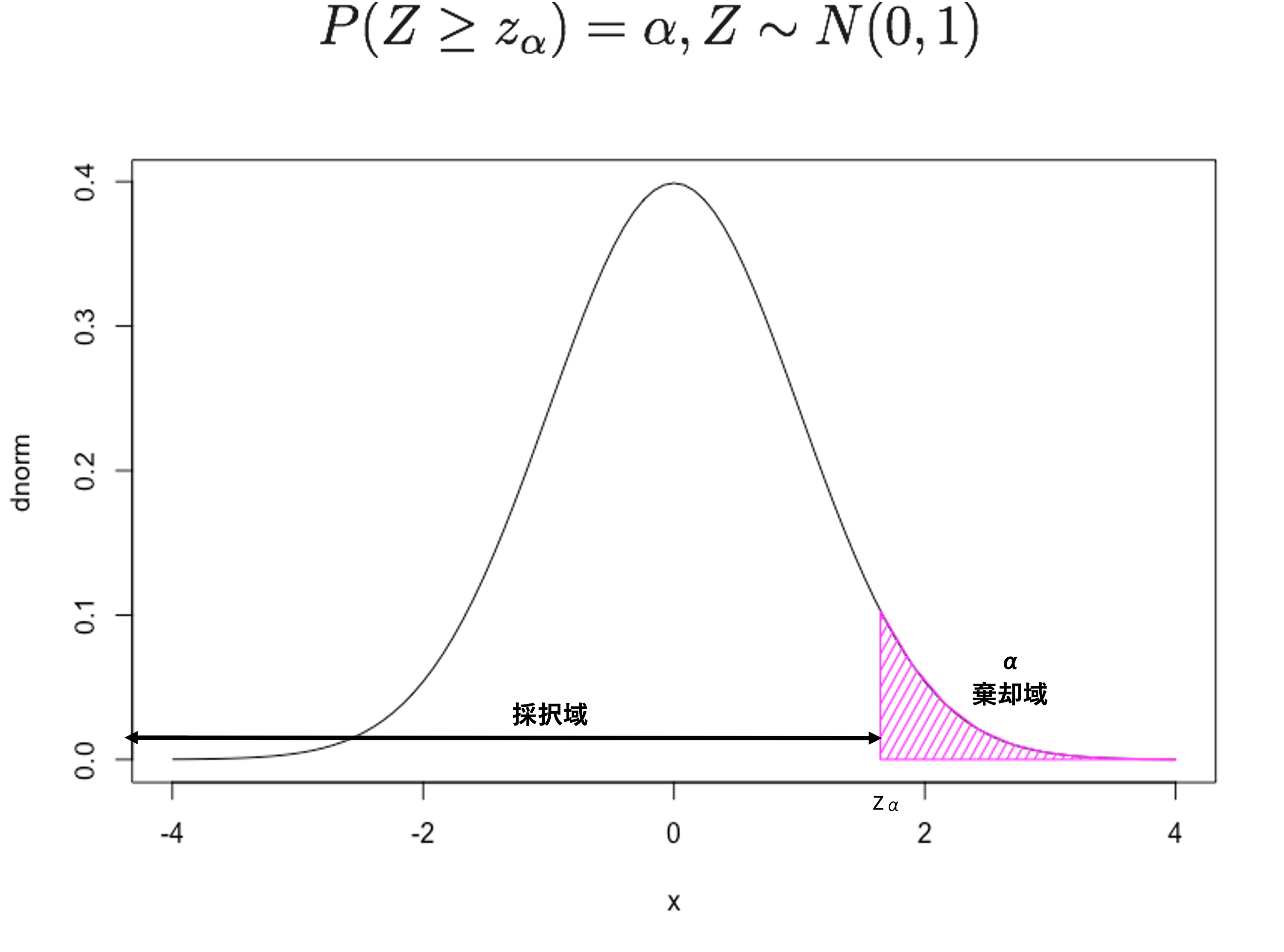
ここで再び話を両側検定に戻し、統計的検定において用いられる有意水準について説明する。ここまでの内容をまとめると、帰無仮説を仮定して検定統計量を計算する場合、帰無仮説が正しければ、棄却域内の値を取る確率は \(\small 100\times \alpha\)%であると言える。そして、検定統計量の計算結果が棄却域に含まれる場合、帰無仮説を棄却するという判断を下す。そのため、統計的に帰無仮説を棄却したからと言って、その結果が必ず正しいとは言い切れない。統計的検定には、根本的に第一種の誤り(Type 1 error)と第二種の誤り(Type 2 error)という二種類の誤りの可能性が内包されている。
第一種の誤りとは、帰無仮説が真であるにも関わらず、帰無仮説を棄却してしまう誤りである。一方で第二種の誤りは、帰無仮説が真ではないのにも関わらず、帰無仮説を採択してしまう誤りである。例えば、ある薬に期待される効果があるかどうかを検証する場合を考える。この時、帰無仮説は「投薬による効果がない」、対立仮説は「投薬による効果がある」と設計する。この場合における第一種の誤りとは、「本当は効き目のない薬を効くと判断してしまう誤り」であり、第二種の誤りとは、「本当は効き目のある薬を聞かないと判断したしまう誤り」である。
| H0が真 | H0が偽 | |
|---|---|---|
| H0を棄却 | Type 1 error | ✓ |
| H0を採択 | ✓ | Type 2 error |
どちらの誤りも見過ごすことのできないものではあるが、第一種の誤りによる損失と、第二種の誤りによる損失を比較し、一般的な統計的検定においては、第一種の誤りの確率を下げることに注視する。なお、研究によっては下記にある検定力という指標に着目し、第二種の誤りに対応した議論を提示することもあるが、本書では割愛する。仮説検定では特に、第一種の誤りの確率を有意水準 \(\small \alpha\) と設定し分析する。また有意水準は、先述の通り棄却域の特定に用いられる。つまり、統計的仮説検定とは、帰無仮説が正しいと仮定した上で有意水準 \(\small \alpha\) の分だけ第一種の誤りの確率を許容したうえで仮説が正しいか否かを確認する作業である。
上記の統計的検定に関わる誤りは、\(\small T_0\) は統計量 T の観測値、Rは\(\small H_0\) の棄却域、Aは\(\small H_0\)の採択域とし、以下のように示される。
有意水準: \(\alpha\) \[ P(T_0\in R|H_0~\text{is True})=\alpha \]
第二種の誤りの確率: \(\beta\) \[ P(T_0\in A|H_0~\text{is False})=\beta \]
検定力: \(1 - \beta\) \[ P(T_0\in R|H_0~\text{is False})=1-\beta \]
ここで、先程の新型電球の例に対し、仮説検定に関わる有意水準を \(\small \alpha=0.05\) と設定し、適応する。帰無仮説が正しいという条件のもとで、帰無仮説を棄却する確率であるため、有意水準は以下のように示すことができる。
\[ \alpha=P(|Z|>c|\mu=1700) =0.05 \] しかしながら、このままだと確率計算が複雑になるため、上式を以下のように書き換える。
\[ 1-\alpha=P(|Z|\leq c|\mu=1700) = \int^c_{-c}f(Z)dZ~_{|\mu=1700}=0.95 \] 再掲になるが、上式の関係を表した図が、以下のものになる。

このとき、検定統計量 Z は帰無仮説が正しければ標準正規分布に従うはずである。したがって、臨界値 \(\pm c\) は、\(\pm z_{0.025}\) として分布表などより導出が可能である。Rにおいては前節と同様、qnorm() により、\(z_{0.025}=1.96\) だとわかる。すなわち、検定統計量の計算結果が 1.96(-1.96)を上回る(下回る)場合には、帰無仮説を棄却するが、そこには第一種の誤りを犯す確率が5%残されていると解釈できる。
ここまでの議論を踏まえ、新型電球に関する統計的検定を標準正規分布に基づき以下のように実施する。
n <- length(bulb)
z <- qnorm(0.025, lower.tail=FALSE)
xbar <- mean(bulb)
sigma <- 180
mu <- 1700
#Test statistic
Z <- (xbar - mu)/(sigma/sqrt(n))
Z## [1] 2.993056分析の結果、検定統計量 Z の実現値が5%有意水準に基づく臨界値(1.96)よりも大きいことが示されたため、5%有意水準で帰無仮説が棄却された。つまり、5%の第一種の誤りの確率を残した上ではあるが、新型電球の製品寿命は旧型製品の寿命よりも長いと言える。このような結果は一般的に、「統計的に有意な結果」と表現される。
ここまでは、有意水準の意味を踏まえ、検定の手順及び結果の解釈について説明した。上述の例では、ある有意水準のもと帰無仮説を棄却できる「統計的に有意な」結果を得た。しかしながら、統計的に有意でない(帰無仮説を棄却できない)結果を得たときには、その解釈について注意が必要である。具体的には、統計的に有意でないからと言って、帰無仮説が正しい(つまり \(\small \mu =1700\) である)と結論づけることはできない。ここまでの説明の通り、有意水準とは第一種の誤りを犯す確率であり、有意水準に基づく統計的検定では主にこの確率に対応した分析を行っている。そのため、第二種の誤りである、本当は \(\small \mu \neq 1700\) であるにも関わらず、\(\small \mu =1700\) と判断している可能性については未対応である。これらの点から「有意でない」ということを理由に、帰無仮説が正しいと結論づけることは適切ではない。そのため、もし今回の仮説検定で帰無仮説を棄却できていなかったとしたら、その結論は「新型電球寿命の平均は1700時間ではないとは言えない」となる。なんとも歯切れの悪い結論だということは理解できるが、統計的検定の特性上、このような解釈を提示しないといけない。
なお、この電球の例のように母集団の分散が既知の場合、検定統計量は標準正規分布に従うと仮定できる。 しかし母集団の分散が未知の場合は、信頼区間での議論と同様、標準偏差の不偏推定量を用いて、自由度 n-1 の t 分布を仮定した分析を行う。そして、t分布に基づく母平均に関する検定を一般的に「t検定(t-test)」と呼ぶ。
なお、t.test() を用いた分析例でも紹介したが、R (他のソフトウェアでも)で統計的検定を実行すると “p-value”(p値)という値を得る。p値については、もう少し詳しい説明が必要であり、解釈にも注意が必要である。
p値は、計算された検定統計量の実現値を臨界値とし、有意水準を計算していると解釈できるが、棄却域と有意水準の関係に基づきもう少し詳細に述べると、以下のように説明することができる(cf. 西山など, 2019)。有意水準を小さく取ると、棄却域は狭くなる。例えば、ある仮説検定において、5%有意水準では帰無仮説を棄却できるが、1%ではできない場合がある。計算された検定統計量の実現値に基づき、有意水準を変えながら検定を行っていくと、これ以上有意水準を小さくすると帰無仮説が棄却されなくなるという有意水準の限界を見つけることができる。この限界をp値と呼ぶ。そのため、p値によって示されている確率は有意水準と同様のものを捉えているのだが、その計算過程が異なるという点において注意が必要である。
ここで改めて、標準正規分布を用いた母平均の検定に着目し、統計的仮説検定についてのより一般的な説明を提示する。\(\small X_1,..,X_n\) を正規母集団 \(N(\mu, \sigma^2)\) からのサンプルサイズ n の無作為標本とする。このとき、帰無仮説の下でのパラメータの値を\(\mu_0\)として、以下の帰無仮説と対立仮説を設計する。
\[ H_0:~\mu=\mu_0,~~~H_1:~\mu\neq\mu_0 \] このとき、検定統計量 Z を以下のように定義する。
\[ Z=\frac{\bar{X}-\mu_0}{\sqrt{\sigma^2/n}} \] そのうえで、有意水準 \(\small \alpha\) に基づく両側臨界値 \(\pm z_{\alpha/2}\) を設定し、以下の方式で検定する。
\[ \begin{cases} |Z|>z_{\alpha/2} & \Rightarrow \text{H0を棄却する。}\\ |Z|\leq z_{\alpha/2} & \Rightarrow \text{H0を採択する。} \end{cases} \]
平均 \(\small \mu\)、分散 \(\small \sigma^2/n\)の正規分布↩︎